因式分解:8x3y3-2xy.
(1)解方程:16(x+1)2 -1=0
(2)-(x-3)3=27
(3)先化简,再求值: ,其中
,其中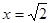 .
.
(4)实数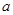 、
、 在数轴上的位置如图所示,请化简:
在数轴上的位置如图所示,请化简: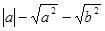 .
.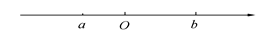
(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E .求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120º得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
阅读理解:“分割、拼凑法”是几何证明中常用的方法。苏科版八上数学第一章《全等三角形》中,有以下两道题,其中问题1中的图1分割成两个全等三角形,而问题2是“HL定理”的证明,却将图2两个直角三角形拼成了一个等腰三角形图3.
请按照上面的思路,补全问题1、2的解答:
问题1:已知:如图1,在△ABC中,AB=AC.求证:∠B=∠C.
问题2:如图2,在△ABC和△A1B1C1中,∠C=∠C1=90°,AB=A1B1,AC=A1C1.
求证:△ABC≌△A1B1C1(补全证明过程) .
证明:把两个直角三角形如图3所示拼在一起.
仿照上面的方法解答问题:
问题3:如图4,△ABC中,∠ACB=90°,四边形CDEF是正方形,AE=5,BE=3.
求阴影部分的面积和.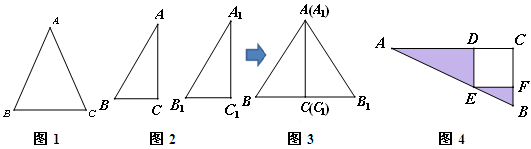
已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
(1)求证:△AEF≌△AEB;
(2)∠DFE= °.
操作题:
(1)已知:∠AOB,点M、N.
求作:①∠AOB的平分线OC;
②点P,在OC上,且PM=PN.(用尺规作图,保留作图痕迹,不写作法)
(2)如图,在3×3网格中,已知线段AB、CD,以格点为端点画一条线段,使它与AB、CD组成轴对称图形.(画出所有可能)