如图,有一壁画,最高点A处离地面4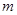 ,最低点B处离地面2
,最低点B处离地面2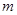 ,若从离地面高
,若从离地面高 的C处观赏它,则离墙多远的视角
的C处观赏它,则离墙多远的视角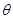 最大?
最大?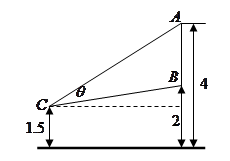
在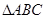 中,角
中,角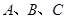 所对的边分别为
所对的边分别为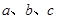 ,已知
,已知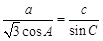 ,
,
(Ⅰ)求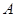 的大小;
的大小;
(Ⅱ)若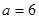 ,求
,求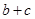 的取值范围.
的取值范围.
已知数列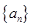 的前
的前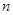 项和是
项和是 ,且
,且 .求数列
.求数列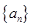 的通项公式;
的通项公式;
若x,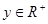 ,且
,且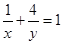 ,求u=x+y的最小值.
,求u=x+y的最小值.
已知数列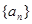 满足:
满足: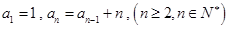 .
.
(Ⅰ)求数列的通项公式;
(Ⅱ)设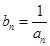 ,求数列
,求数列 的前
的前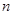 项和
项和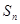 .
.
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米.已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元.
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米的平均开发费用最低,该写字楼应建为多少层?