如图,某观测站 在城
在城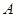 的南偏西
的南偏西 的方向上,由
的方向上,由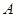 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东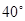 ,在
,在 处测得距
处测得距 为31公里的公路上
为31公里的公路上 处,有一人正沿公路向
处,有一人正沿公路向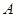 城走去,走了20公里后,到达
城走去,走了20公里后,到达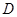 处,此时
处,此时 、
、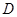 间距离为
间距离为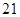 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达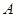 城.
城.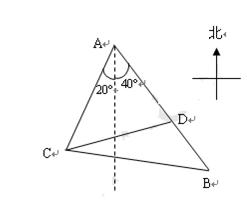
如图,在直三棱柱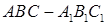 中,底面
中,底面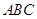 为等边三角形,且
为等边三角形,且 ,
,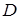 、
、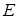 、
、 分别是
分别是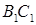 ,
,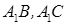 的中点.
的中点.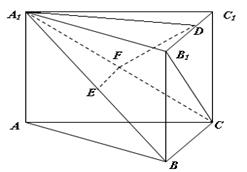
(1)求证: ∥
∥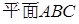 ;
;
(2)求证: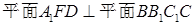 ;
;
(3) 求直线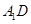 与平面
与平面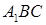 所成的角.
所成的角.
(理)已知点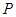 是圆
是圆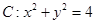 上的动点.
上的动点.
(1)求点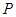 到直线
到直线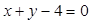 的距离的最小值;
的距离的最小值;
(2)若直线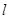 与圆
与圆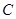 相切,且
相切,且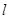 与x,y轴的正半轴分别相交于
与x,y轴的正半轴分别相交于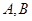 两点,求
两点,求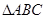 的面积最小时直线
的面积最小时直线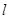 的方程;
的方程;
(文)已知圆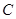 和
和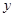 轴相切,圆心在直线
轴相切,圆心在直线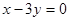 上,且被直线
上,且被直线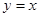 截得的弦长为
截得的弦长为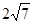
 ,求圆
,求圆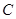 的标准方程。
的标准方程。
已知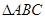 三边所在直线方程
三边所在直线方程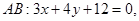
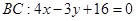 ,
,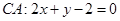 ,求
,求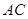 边上的高所在的直线方程.
边上的高所在的直线方程.
(本题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.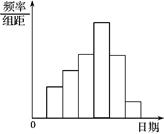
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪一组获奖率较高?