将长为1，宽为a的长方形纸片
如图左那样折一下，剪下一个边长等于长方形宽度的正方形（称为第一次操作）；再把剩下的长方形如图右那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）．
（1）第一次操作后，剩下的长方形的长和宽分别为多少？（用含a的代数式表示）
（2）第二次操作后，剩下的长方形的面积是多少？（列出代数式，不需化简）
（3）假如第二次操作后，剩下的长方形恰好是正方形，则a的值是多少？
甲口袋中装有两个相同的小球，它们的标号分别为2和7，乙口袋中装有两个相同的小球，它们的标号分别为4和5，丙口袋中装有三个相同的小球，它们的标号分别为3，8，9．从这3个口袋中各随机地取出1个小球．
（1）求取出的3个小球的标号全是奇数的概率是多少？
（2）以取出的三个小球的标号分别表示三条线段的长度，求这些线段能构成三角形的概率．
求不等式组
的整数解．
如图，已知D是△ABC的边AB上一点，CE∥AB，DE交
AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．
先化简，再求值：
，其中 x=
．
（11·贵港）．
如图，已知直线y＝－
x＋2与抛物线y＝a (x＋2) 2相交于A、B两点，点A在y轴上，M为抛物线的顶点．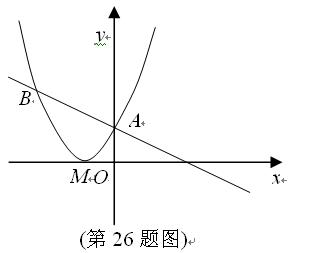
（1）请直接写出点A的坐标及该抛物线的解析式；
（2）若P为线段AB上一个动点（A、B两端点除外），连接PM，设线段PM的长为l，点P的横坐标为x，请求出l2与x之间的函数关系，并直接写出自变量x的取值范围；
（3）在（2）的条件下，线段AB上是否存在点P，使以A、M、P为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．