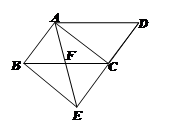请你先认真阅读材料:
计算(-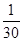 )÷(
)÷(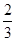 一
一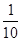 +
+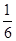 -
-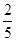 ).
).
解法l: 解法2:
(-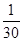 )÷(
)÷(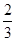 一
一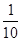 +
+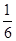 -
-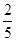 ) 原式的倒数为:
) 原式的倒数为:
=(-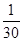 )÷[(
)÷[(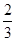 +
+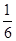 )-(
)-(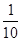 +
+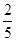 )] (
)] (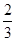 一
一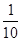 +
+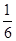 -
-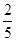 )÷(-
)÷(-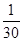 )
)
=(-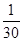 )÷(
)÷( -
-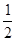 ) =(
) =(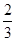 一
一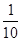 +
+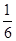 -
-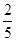 )×(-30)
)×(-30)
=(-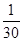 )÷
)÷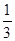 =-20+3-5+12
=-20+3-5+12
=-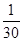 ×3 =(-20-5)+(3+12)
×3 =(-20-5)+(3+12)
=-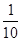 =-10
=-10
故原式=-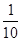
再根据你对所提供材料的理解,选择合适的方法计算:
(一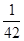 )÷(
)÷(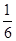 一
一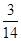 +
+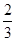 -
-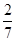 ).
).
某商业公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的销售和生产进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图1);一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示,其中6月份成本最高(如图2).
(1)一件商品在3月份出售时的利润是多少元?(利润=售价-成本)
(2)求图2中表示一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30000件,请你计算一下该公司在一个月内最少获利多少元?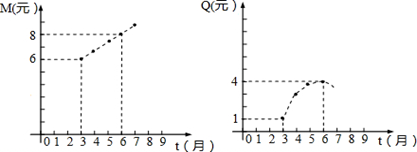
如图:已知正方形ABCD的对角线AC长为20cm,半径为1的⊙O1的圆心O1从A点出发以1cm/s的速度向C运动,半径为1的⊙O2的圆心O2从C点出发以2cm/s的速度向A运动且半径同时也以1cm/s的速度不断增大,两圆同时运动,当其中一个圆的圆心运动到AC的端点时,另一个圆也停止运动.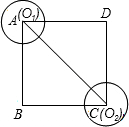
(1)当O1运动了几秒时,⊙O1与AD相切?
(2)当O2运动了几秒时,⊙O2与CB相切?
(3)当O2运动了几秒时,⊙O1与⊙O2相切?
矩形ABCD中,AD=5,AB=3,将矩形ABCD沿某直线折叠,使点A的对应点A′落在线段BC上,再打开得到折痕EF.
(1)当A′与B重合时(如图1),EF=;当折痕EF过点D时(如图2),求线段EF的长;
(2)观察图3和图4,设BA′=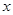 ,①当
,①当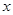 的取值范围是时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.
的取值范围是时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.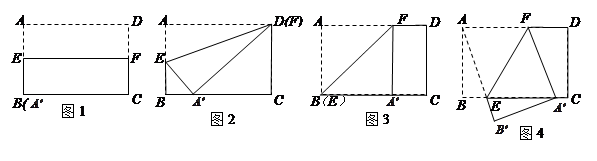
已知关于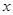 的一元二次方程
的一元二次方程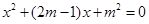 有两个实数根
有两个实数根 和
和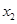 .
.
(1)求实数 的取值范围;(2)当
的取值范围;(2)当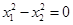 时,求
时,求 的值.
的值.
如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.⑴求证:△ABF≌△ECF
⑵若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.