现一居民小区的圆柱形自来水管破裂，要及时更换，为此施工人员需知道水管的半径.如图，是水平放置的受损的自来水管管道截面图.（阴影部分为水）.
⑴请用直尺、圆规补全水管的圆形截面图；（不写作法，但应保留作图痕迹）
⑵若水面宽AB=24cm，水面最深处为6cm，试求水管的半径.
如图，矩形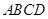
是供一辆机动车停放的车位示意图．请你参考图中数据，计算车位所占街道的宽度
．
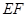（参考数据：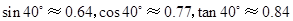
，结果精确到
．）
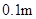某服装厂准备加工300套演出服．在加工60套后，采用了新技术，使每天的工作效率是原来的2倍，结果共用9天完成任务．求该厂原来每天加工多少套演出服．
小刚想给小东打电话，但忘了电话号码中的一位数字，只记得号码是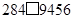
（
表示忘记的数字）．
（1）若小刚从
至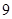
的自然数中随机选取一个数放在位置，则他拨对小东电话号码的概率是 ．
（2）若位置的数字是不等式组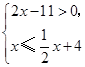
的整数解，求可能表示的数字．
下面的两个网格中，每个小正方形的边长均为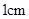
．请你分别在每个网格中画出一个顶点在格点上，且周长为
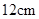的形状和大小不同的凸多边形．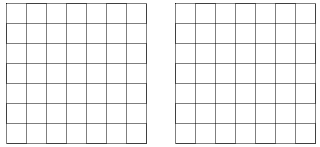
计算：
．