.已知向量 满足
满足
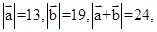 求
求
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合(如图)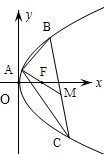
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标
(3)求BC所在直线的方程.
(本小题满分14分)设函数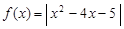 。
。
(1)在区间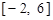 上画出函数
上画出函数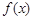 的图像;
的图像;
(2)设集合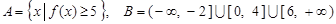 .试判断集合
.试判断集合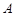 和
和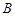 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当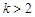 时,求证:在区间
时,求证:在区间 上,
上,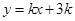 的图像位于函数
的图像位于函数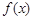 图像的上方.
图像的上方.
(本小题满分14分)已知函数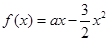 的最大值不大于
的最大值不大于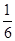 ,
,
(1)求实数a的取值范围;
(2)当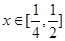 时.
时.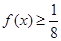 ,求实数a的值。
,求实数a的值。
(本小题满分14分)若函数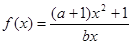 ,且
,且 ,
,
(1)求 的值,写出
的值,写出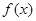 的表达式 ;
的表达式 ;
(2)判断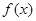 在
在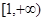 上的增减性,并加以证明.
上的增减性,并加以证明.
(本小题满分14分)已知集合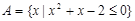 ,
, ,
,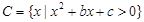 ,并且满足
,并且满足 ,
, ,求
,求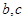 的值。
的值。