(本小题满分15分)
数列 是首项为23,公差为整数的等差数列,且
是首项为23,公差为整数的等差数列,且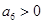 ,
, .
.
求:(1)数列 的公差;
的公差;
(2)前 项和
项和 的最大值;
的最大值;
(3)当 时,求
时,求 的最大值.
的最大值.
(本小题满分12分)
双曲线 与双曲线
与双曲线 有共同的渐近线,且经过点
有共同的渐近线,且经过点 ,椭圆
,椭圆 以
以
双曲线 的焦点为焦点且椭圆上的点与焦点的最短距离为
的焦点为焦点且椭圆上的点与焦点的最短距离为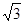 ,求双曲线
,求双曲线 和椭圆
和椭圆 的方程。
的方程。
(本小题满分12分)
某工厂计划生产甲、乙两种产品,这两种产品都需要两种原料。生产甲产品1工时需要A种原料3kg,B种原料1 kg;生产乙产品1工时需要A种原料2kg,B种原料2kg。现有A种原料1200 kg,B种原料800 kg。如果生产甲产品每工时的平均利润是30元,生产乙产品每工时的平均利润是40元,问甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?
(本小题满分12分)
在 中内角
中内角 的对边分别为
的对边分别为 ,且
,且
(1)求 的值;
的值;
(2)如果b=4 ,且a=c,求
,且a=c,求 的面积.
的面积.
(本小题满分10分)
已知 ,解关于
,解关于 的不等式
的不等式 <
<
(本小题满分12分)
已知数列 满足
满足 ,数列
,数列 满足
满足 ,
,
数列 满足
满足 .
.
(1)若 ,证明数列
,证明数列 为等比数列;
为等比数列;
(2)在(1)的条件下,求数列 的通项公式;
的通项公式;
(3)若 ,证明数列
,证明数列 的前
的前 项和
项和 满足
满足 。
。