设A= ,则矩阵A的一个特征值λ和对应的一个特征向量
,则矩阵A的一个特征值λ和对应的一个特征向量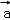 为()
为()
A.λ=3,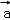 =( =(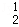 ) ) |
B.λ=﹣1,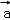 =( =(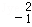 ) ) |
C.λ=3,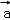 ( ( ) ) |
D.λ=﹣1,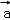 =( =(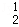 ) ) |
方程组 的增广矩阵是()
的增广矩阵是()
A. |
B. |
C. |
D. |
关于x、y的二元一次方程组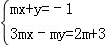 的系数行列式D=0是该方程组有解的()
的系数行列式D=0是该方程组有解的()
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |
已知关于x,y的二元一次线性方程组的增广矩阵为 ,记
,记 ,则此线性方程组有无穷多组解的充要条件是()
,则此线性方程组有无穷多组解的充要条件是()
A.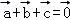 |
B. 两两平行 两两平行 |
C.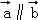 |
D. 方向都相同 方向都相同 |
下列四个算式:
①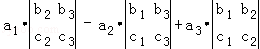 ;
;
② ;
;
③a1b2c3+a2b3c1+a3b1c2﹣a1b3c2﹣a2b1c3﹣a3b2c1;
④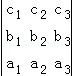
其中运算结果与行列式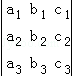 的运算结果相同的算式有()
的运算结果相同的算式有()
| A.1个 | B.2个 | C.3个 | D.4个 |