某次足球比赛的记分规则如下:胜一场得3分,平一场得1分,负一场是0分.某队踢了14场,其中负5场,共得19分.若设胜了x场,平了y场.
如图,在△ABC中,∠ACB=90º,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF//AB交直线DE于F.设CD=x.
(1)当x取何值时,四边形EACF是菱形?请说明理由;
(2)当x取何值时,四边形EACF的面积等于3?
直线y=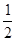 x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
x+2与x轴、y轴分别交于A、B两点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标;
(2)求S与x的函数关系式;
(3)当S=12时,求点D的坐标.
下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题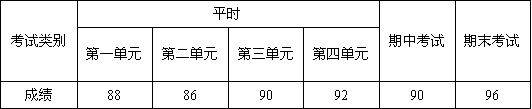
(1)李刚同学6次成绩的极差是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
(4)利用图的权重计算一下李刚本学期的综合成绩(平时成绩用四次成绩的平均数写出解题过程,每次考试满分都是100分)
已知圆O的直径AB、CD互相垂直,弦AE交CD于F,若圆O的半径为R.
求证:AE·AF=2 R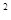 .
.
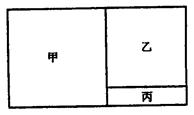
如图,有一长方形的地,长为x米,宽为120米,建筑商将它分成三部分:甲、乙、丙.甲和乙为正方形.现计划甲建设住宅区,乙建设商场,丙开辟成公司.若已知丙地的面积为3200平方米,试求x的值.