海岛O上有一座海拔1000m的山,山顶上设有一个观察站A,上午11时测得一轮船在岛北偏东60o的C处,俯角为30o,11时10分又测得该船在岛北偏西60o的B处,俯角为60o,如图所示,求:
(1)该船的速度为每小时多少千米?
(2)若此船以匀速度继续航行,则它何时到达岛的正西方向?此时,船所在点E离开海岛多少千米?
已知两点A(-2,0)、B(0,2),点C是圆x2+y2-2x=0上的任意一点,则△ABC面积的最小值是 ( )
A.3-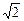 |
B.3+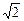 |
C.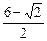 |
D. |
已知双曲线 的右焦点为F,若过点F且倾斜角为30°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是()
的右焦点为F,若过点F且倾斜角为30°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是()
A.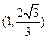 |
B. |
C. |
D.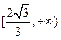 |
椭圆 +
+ =1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于()
=1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于()
| A.2 | B.4 |
| C.6 | D.8 |
若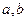 是异面直线,且
是异面直线,且 //平面
//平面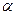 ,那么
,那么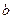 与平面
与平面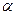 的位置关系是()
的位置关系是()
A.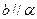 |
B.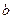 与 与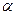 相交 相交 |
C. |
D.以上三种情况都有可能 |
下列四个命题中正确命题的个数是 ( )
(1)三点确定一个平面
(2)若点P不在平面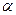 内,A、B、C三点都在平面
内,A、B、C三点都在平面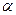 内,则P、A、B、C四点不共面
内,则P、A、B、C四点不共面
(3)两两相交的三条直线在同一平面内
(4)两组对边分别相等的四边形是平面图形
A、0 B、1 C、2 D、3