摩天大楼中一部直通高层的客运电梯，行程超过百米。电梯的简化模型如图1所示。考虑安全、舒适、省时等因素，电梯的加速度a随时间t变化的。已知电梯在t＝0时由静止开始上升，a-t图如图2所示。电梯总质量m＝2.0´103kg。忽略一切阻力，重力加速度g取10m/s2。
（1）求电梯在上升过程中受到的最大拉力F1和最小拉力F2；
（2）类比是一种常用的研究方法。对于直线运动，教科书中讲解由v-t图像求位移的方法。请你借鉴此方法，对比加速度和速度的定义，根据图2所示a-t图像，求电梯在第1s内速度改变量Dv1和第2s的速率v2；
（3）求电梯以最大速率上升时，拉力做功的功率P；再求在0-11s时间内，拉力和重力对电梯所做的总功W。
如图所示，质量为5 kg的物块在水平拉力F="15" N的作用下,从静止开始向右运动.物体与水平地面间的动摩擦因数μ=0.2.求: 在力F的作用下,物体在前10 s内的位移；（g取10 m/s2）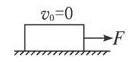
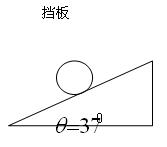
如图所示，一个质量为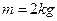
的均质小球放在倾角为
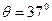的光滑斜面上，并被斜面上一个竖直的光滑挡板挡住，处于静止状态，试求小球对挡板和斜面的压力（已知
）
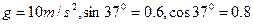如图所示，半径R=0.80m的
光滑圆弧轨道竖直固定，过最低点的半径OC处于竖直位置，其右方有底面半径r=0.2m的转筒，转筒顶端与C等高，下部有一小孔，距顶端h=1m，转筒的轴线与圆弧轨道在同一竖直平面内，开始时小孔也在这一平面内的图示位置．现使一质量m=0.1kg的小物块自A点由静止开始下落后打在圆弧轨道上的B点但不反弹，在瞬间碰撞过程中，小物块沿半径方向的分速度立刻减为0，沿切线方向的分速度不变．此后，小物块沿圆弧轨道滑下，到达C点时触动光电装置，使转筒立刻以某一角速度匀速转动起来，且小物块最终正好进入小孔．已知A、B到圆心O的距离均为R，与水平方向的夹角均为θ=30°，不计空气阻力，g取l0m/s2，求：
（1）小物块刚下落到B点时，在与B点碰撞前的瞬时速度的大小；
（2）小物块到达C点时对轨道的压力大小FC；
（3）转筒轴线距C点的距离L；
（4）转筒转动的角速度ω.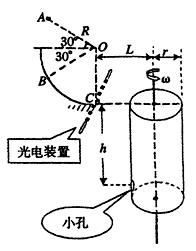
如图所示，光滑水平面上有一块木板，质量M = 1.0 kg，长度L=" 1.0" m．在木板的最左端有一个小滑块（可视为质点），质量m = 1.0 kg．小滑块与木板之间的动摩擦因数μ = 0.30．开始时它们都处于静止状态．某时刻起对小滑块施加一个F =" 8.0" N水平向右的恒力，此后小滑块将相对木板滑动. g取l0m/s2，求：
（1）小滑块和木板的加速度大小；
（2）小滑块离开木板时的速度大小；
（3）要使小滑块在木板上滑动时的速度始终是木板速度的2倍，需将恒力F改为多大？
在5m高处以10m/s的速度水平抛出一小球，不计空气阻力，g取10m/s2，求：
（1）小球在空中运动的时间；
（2）小球落地时的水平位移大小；