伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次。假设某次试验伽利略是这样做的:在斜面上任取三个位置A、B、C,让小球分别由A、B、C滚下,如图所示。设A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3, 小球由A、B、C运动到斜面底端时的速度分别为v1、v2、v3,则下列关系式中正确,并且是伽利略用来证明小球沿光滑斜面向下的运动是匀变速直线运动的是( )
A.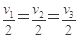 B.
B.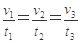
C.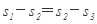 D.
D.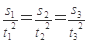
关于惯性,下列说法正确的是
| A.静止的物体没有惯性,运动的物体才有惯性 |
| B.物体的质量越大,惯性越大 |
| C.正在行驶的两辆汽车,行驶快的不易停下来,所以速度大的物体惯性大 |
| D.自由下落的物体处于完全失重状态,物体的惯性消失 |
如图所示的水平面上,橡皮绳一端固定,另一端连接两根弹簧,连接点P在F1、F2和F3三力作用下保持静止。下列判断正确的是
| A.F1> F2>F3 | B.F2>F3> F1 |
| C.F3>F1> F2 | D.F3>F2> F1 |
如图所示,跳水运动员踩压跳板使跳板弯曲到最低点时,下列说法正确的是
| A.跳板发生形变,运动员的脚没有发生形变 |
| B.运动员受到的支持力,是跳板发生形变而产生的 |
| C.此时跳板对运动员的支持力和运动员的重力等大 |
| D.此时跳板对运动员的支持力大于运动员对跳板的压力 |
物体做直线运动的位移s与时间t的关系为s =" 5t+" t 2,则该物体
| A.物体运动的初速度是5m/s |
| B.物体运动的加速度是1m/s2 |
| C.第1s内的位移是5m |
| D.任意相邻1s内的位移差都是1m |
关于自由落体运动,下列说法正确的是
| A.自由落体运动是物体不受任何作用力的运动 |
| B.从静止开始出发的运动就是自由落体运动 |
| C.重力加速度的方向总是竖直向下 |
| D.自由落体运动的速度和加速度均逐渐增大 |