如图所示，光滑水平面上有一质量M=4.0kg的带有圆弧轨道的平板车，车的上表面是一段长L=1.0m的粗糙水平轨道，水平轨道左侧连一半径R="0.25m" 的
光滑圆弧轨道，圆弧轨道与水平轨道在O′点相切。车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧，一质量m=1.0kg的小物块紧靠弹簧放置，小物块与水平轨道间的动摩擦因数μ=0.5。整个装置处于静止状态，现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A。取g=10m/2，求：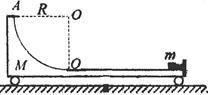
(1) 小物块到达A点时，平板车的速度大小
(2) 解除锁定前弹簧的弹性势能；
(3) 小物块第二次经过O′点时的速度大小；
(4) 小物块与车最终相对静止时，它距O′点的距离。
公共汽车从车站由静止以1 m/s2的加速度匀加速开出,司机发现有乘客未上车,急忙刹车.车匀减速停下,整个过程历时5s,车前进了10m，求
（1）汽车在此过程中最大速度
（2）匀加速运动的时间
（3）匀减速运动的加速度
某物体做单向直线运动，以速度v1运动了1/4的路程，接着以速度v2="20" km/h完成了其余的3/4，如果运动员全程的平均速度为v="16" km/h，求v1的值
电动车以40 m/s的速度行驶，刹车后得到的加速度大小为4m/s2，从刹车开始，求经12S，电动车通过的位移是多少？
一辆小汽车通过长1100米的隧道，小汽车刚进隧道时的速度是10m/s，出隧道时的速度是12m/s，(小汽车可看成质点)求：
（1）小汽车过隧道时的加速度是多大？
2）通过隧道所用的时间是多少？
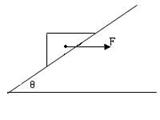
如图所示，一木块质量为m，放在倾角为θ的静止斜面上，木块间的动摩擦因数为μ，当用一水平方向的力F推这木块时，木块沿斜面匀速上升，请画出受力分析图并求这水平作用力F的大小。