质谱仪的工作原理图如图所示,A为粒子加速器,加速电压为U1;M为速度选择器,两板间有相互垂直的匀强磁场和匀强电场,匀强磁场的磁感应强度为B1,两板间距离为d;N为偏转分离器,内部有与纸面垂直的匀强磁场,磁感应强度为B2.一质量为m,电荷量为q的带正电的粒子由静止经加速器加速后,恰能通过速度选择器,进入分离器后做圆周运动,并打到感光板P上.不计重力,求: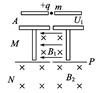
(1)粒子经粒子加速器A加速后的速度v的大小及速度选择器M两板间的电压U2.
(2)粒子在偏转分离器N的磁场中做圆周运动的半径R.
(3)某同学提出在其他条件不变的情况下,只减小加速电压U1,就可以使粒子在偏转分离器N的磁场中做圆周运动的半径减小.试分析他的说法是否正确.
一辆载重汽车质量104kg,汽车初速度为4 m/s,经5s后速度达到了10m/s。设这一过程中汽车做匀加速直线运动,已知汽车所受阻力f=5×103N,取g=10m/s2,求:
(1)汽车在此过程中的加速度大小;
(2)汽车发动机的牵引力大小。
如图所示为质谱仪的原理图,A为粒子加速器,电压为U1;B为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;C为偏转分离器,磁感应强度为B2。今有一质量为m、电量为q的正离子经加速后,恰好通过速度选择器,进入分离器后做匀速圆周运动,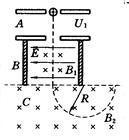
求:(1)粒子的速度v;
(2)粒子在B2磁场中做匀速圆周运动的半径R。
如图所示,水平放置的平行板电容器,极板长L= 0.1m,两板间距离d =" 0.4" cm。有一带电微粒以一定的初速度从两板中央平行于极板射入,若板间不加电场,由于重力作用微粒恰能落到下板中点O处;若板间加竖直方向的匀强电场,带电微粒刚好落到下板右边缘B点。已知微粒质量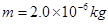 ,电量
,电量 ,取g=10m/s2。
,取g=10m/s2。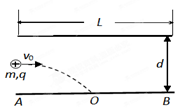
试求:(1)带电微粒入射初速度的大小;
(2)板间所加电场的电场强度多大?方向怎样?
如图所示,将电荷量为q=3.0×10-9C的点电荷从匀强电场中的A点移动到B点,AB=2cm,电场力做的功为6.0×10-7J,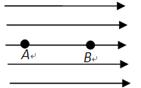
(1)若以B点为零电势点,求A点的电势和A、B两点的电势差;
(2)求匀强电场的场强E
如图所示,左侧匀强电场的区域宽度为L,电场强度为E,右侧匀强磁场的左右宽度为d ,磁场的上下区域很长,一质量为m、带电量为q的粒子,从电场的左边界A点静止释放,经电场加速后垂直进入磁场,出磁场时与入射方向的偏角为θ.(不计粒子重力)
求:
(1)粒子离开电场时的速度;
(2)匀强磁场的磁感应强度;
(3)粒子在磁场中的运动时间.