轻质细线吊着一质量为m=0.42kg,边长为L=1m、匝数n=10的正方形线圈,其总电阻为r=l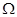 。在框的中间位置以下区域分布着矩形磁场,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,
。在框的中间位置以下区域分布着矩形磁场,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,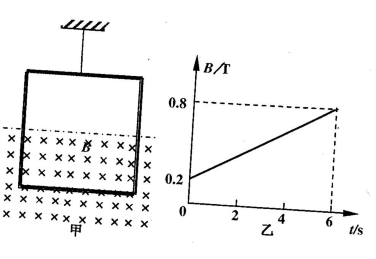
求:
(1)判断线圈中产生的感应电流的方向是顺时针还是逆时针?
(2)线圈的电功率;
(3)在t=4s时轻质细线的拉力大小
光滑水平面上放着质量mA="1" kg的物块A与质量mB="2" kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能Ep="49" J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R="0.5" m,B恰能到达最高点C。取g="10" m/s2,求:
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I的大小;
(3)绳拉断过程绳对A所做的功W。
有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失。碰后B运动的轨迹为OD曲线,如图所示。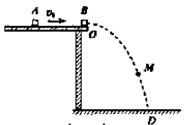
(1)已知滑块质量为m,碰撞时间为 ,求碰撞过程中A对B平均冲力的大小。
,求碰撞过程中A对B平均冲力的大小。
(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动,特制做一个与B平抛轨迹完全相同的光滑轨道,并将该轨道固定在与OD曲线重合的位置,让A沿该轨道无初速下滑(经分析,A下滑过程中不会脱离轨道)。
a.分析A沿轨道下滑到任意一点的动量pA与B平抛经过该点的动量pB的大小关系;
b.在OD曲线上有一M点,O和M两点连线与竖直方向的夹角为45°。求A通过M点时的水平分速度和竖直分速度。
一倾角为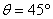 的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?
的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点)。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后,将以原速返回。重力加速度g="10" m/s2。在小物块与挡板的前4次碰撞过程中,挡板给予小物块的总冲量是多少?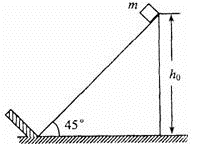
图中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘住物质的固定挡板粘住,在极短的时间内速度减为零。小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点。求
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量;
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小。
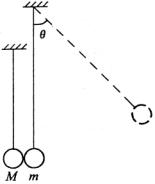
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并挂悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点处与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°。