如图,一半径为R的圆表示一柱形区域的横截面(纸面)。在柱形区域内加一方向垂直于纸面的匀强磁场,一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域,在圆上的b点离开该区域,离开时速度方向与直线垂直。圆心O到直线的距离为  。现将磁场换为平行于纸面且垂直于直线的匀强电场,同一粒子以同样
。现将磁场换为平行于纸面且垂直于直线的匀强电场,同一粒子以同样
速度沿直线在a点射入柱形区域,也在b点离开该区域。若磁感应强度大小为B,不计重力,求:(1)求粒子在匀强磁场中做圆周运动的半径。(2) 电场强度的大小。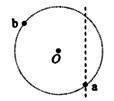
如图,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=  匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,–
匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,– L)的A点以速度v0沿 +x方向射出,恰好经过坐标为[0,-(
L)的A点以速度v0沿 +x方向射出,恰好经过坐标为[0,-( –1)L]的C点射入区域Ⅰ。粒子重力忽略不计。
–1)L]的C点射入区域Ⅰ。粒子重力忽略不计。
(1)求匀强电场的电场强度大小E;
(2)求粒子离开区域Ⅰ时的位置坐标;
(3)要使粒子从区域Ⅱ上边界离开磁场,可在区域Ⅱ内加垂直纸面向内的匀强磁场。试确定磁感应强度B的大小范围,并说明粒子离开区域Ⅱ时的速度方向。
某运动员做跳伞训练,他从悬停在空中的直升飞机上由静止跳下,跳离飞机一段时间后打开降落伞做减速下落。他打开降落伞后的速度图线如图甲所示。降落伞用8根对称的绳悬挂运动员,每根绳与中轴线的夹角均为37°,如图乙。已知人的质量为50 kg,降落伞质量也为50 kg,不计人所受的阻力,打开伞后伞所受阻力Ff与速度v成正比,即Ff=kv (g取10 m/s2,sin 53°=0.8,cos 53°=0.6)。求:
(1)打开降落伞前人下落的距离为多大?
(2)求阻力系数k和打开伞瞬间的加速度a的大小和方向?
(3)悬绳能够承受的拉力至少为多少?
研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间) ,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以
,但饮酒会导致反应时间延长,在某次试验中,志愿者少量饮酒后驾车以 的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。取重力加速度的大小g=10m/s2。求:
的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m。减速过程中汽车位移s与速度v的关系曲线如图乙所示,此过程可视为匀变速直线运动。取重力加速度的大小g=10m/s2。求: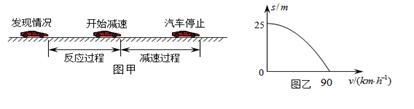
(1)减速过程汽车加速度的大小及所用时间;
(2)饮酒使志愿者的反应时间比一般人增加了多少?
(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值。
公路上行驶的两汽车之间保持一定的安全距离。当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰。通常情况下,人的反应时间和汽车系统的反应时间之和为1s。当汽车在晴天干燥沥青路面上以108km/h的速度匀速行驶时,安全距离为120m,设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120m,求汽车在雨天安全行驶的最大速度。
如图所示,斜面倾角为 ,一质量为
,一质量为 的木块恰能沿斜面匀速下滑,若用一水平恒力F作用于木块上,使之沿斜面向上做匀速运动,求此恒力F的大小。(
的木块恰能沿斜面匀速下滑,若用一水平恒力F作用于木块上,使之沿斜面向上做匀速运动,求此恒力F的大小。( )
)