如图所示,质量为M,长度为L的长木板放在水平桌面上,木板右端放有一质量为m长度可忽略的小木块。开始时木块、木板均静止,某时刻起给木板施加一大小为F方向水平向右的恒定拉力,若最大静摩擦力等于滑动摩擦力。
(1)若地面光滑且M和m相对静止则m受到的摩擦力多大?
(2)若木块与木板之间、木板与桌面之间的动摩擦因数均为μ,拉力F =4μ(m + M)g,求从开始运动到木板从小木块下抽出经历的时间。 
重为100N的物体在细线OA、OB共同作用下处于静止状态,细线OA、OB与水平天花板的夹角分别为30°、60°,如图所示,求:
(1)细线OA的拉力FOA、细线OB的拉力FOB
(2)若细线OA、OB所承受的最大拉力分别为200N、30 0N,为了使细线OA、OB不会被拉断,则物体的重力不能超过多少?
0N,为了使细线OA、OB不会被拉断,则物体的重力不能超过多少?
一辆汽车从O点静止开始做匀加速直线运动,已知在2s内经过相距27m的A、B两点,汽车经过B点时的速度为15m/s。如图所示,求:
(1) 汽车经过A点的速度; (2) A点与出发点间的距离
如图所示,两条平行的金属导轨MP、NQ与水平面夹角为 ,设导轨足够长。导轨处在与导轨平面垂直的匀强磁场中,磁感应强度B=0.80T,与导轨上端相连的电源电动势E=4.5V,内阻r=0.4Ω,水平放置的导体棒ab的电阻R=1.5Ω,两端始终与导轨接触良好,且能沿导轨无摩擦滑动,与导轨下端相连的电阻R1=1.0Ω,电路中其它电阻不计。当单刀双掷开关S与1接通时,导体棒刚好保持静止状态,求:
,设导轨足够长。导轨处在与导轨平面垂直的匀强磁场中,磁感应强度B=0.80T,与导轨上端相连的电源电动势E=4.5V,内阻r=0.4Ω,水平放置的导体棒ab的电阻R=1.5Ω,两端始终与导轨接触良好,且能沿导轨无摩擦滑动,与导轨下端相连的电阻R1=1.0Ω,电路中其它电阻不计。当单刀双掷开关S与1接通时,导体棒刚好保持静止状态,求:
(1)磁场的方向;
(2)S与1接通时,导体棒的发热功率;
(3)当开关S与2接通后,导体棒ab在运动过程中,单位时间(1s)内扫过的最大面积。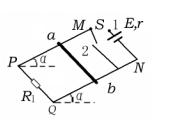
如图所示,在xoy平面内,第I象限中有匀强电场,场强大小为E,方向沿y轴正方向,在x轴的下方有匀强磁场,磁感强度大小为B,方向垂直于纸面向里,今有一个质量为m,电荷量为e的电子(不计重力),从y轴上的P点以初速度v0垂直于电场方向进入电场。经电场偏转后,沿着与x轴正方向成45o进入磁场,并能返回到原出发点P。求:
(1)作出电子运动轨迹的示意图,并说明电子的运动情况。
(2)P点离坐标原点的距离h。
(3)电子从P点出发经多长时间第一次返回P点?
附加题(本题共2小题,共20分。建议重点高中或理科优秀的学 生作答。各学校可根据本校实际情况酌情算分。)
生作答。各学校可根据本校实际情况酌情算分。)
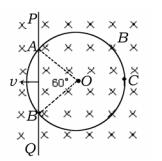
用电阻为18Ω的均匀导线弯成如图所示直径D=0.80m的封闭金属圆环,环上AB弧所对圆心角为60,将圆环垂直于磁感线方向固定在磁感应强度B=0.50T的匀强磁场中,磁场方向垂直于纸面向里。一根每米电阻为1.25Ω的直导线PQ,沿圆环平面向左以 3.0m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
3.0m/s的速度匀速滑行(速度方向与PQ垂直),滑行中直导线与圆环紧密接触(忽略接触处的电阻),当它通过环上A、B位置时,求:
(1)直导线AB段产生的感应电动势,并指明该段直导线中电流的方向;
(2)此时圆环上发热损耗的电功率。