（本题12分）如图，二次函数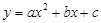
的图象与x轴交于两个不同的点A（－2，0）、B（4，0），与y轴交于点C（0，3），连结BC、AC，该二次函数图象的对称轴与x轴相交于点D．
（1）求这个二次函数的解析式、点D的坐标及直线BC的函数解析式；
（2）点Q在线段BC上，使得以点Q、D、B为顶点的三角形与△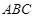
相似，求出点Q的坐标；
（3）在（2）的条件下，若存在点Q，请任选一个Q点求出△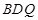
外接圆圆心的坐标．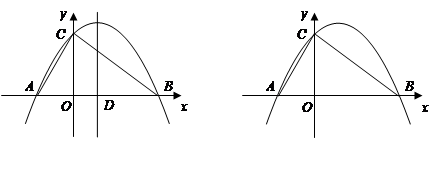
化简与计算：(每小题4分,共12分)
①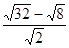
② 
③
如图，一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?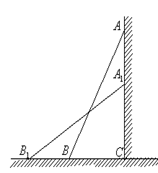
一种盛满饮料的圆柱形杯子,测得内部底面半径为2.5cm,高为12cm,吸管放进杯子里,杯口外面至少要露出4.6cm,问吸管至少要做多长?(5分)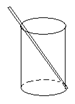
在数轴上画出表示
的点。(3分)
如图，DB∥AC，且DB=
AC，E是AC的中点，
(1
)求证：BC=DE；
(2)连结AD、BE，若要使四边形DBEA是矩形，则给△ABC添加一个什么条件，为什么?
(3)在（2）的条件下，若要使四边形DBEA是正方形，则∠C="" 0