七名学生的体重，以48.0㎏为标准，把超过标准体重的千克计记为正数，不足的千克记为负数，将其体重记录如下表：
| 学生 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 与标准体重之差 |
-3.0 |
+1.5 |
+0.8 |
-0.5 |
+0.2 |
+1.2 |
+0.5 |
（1）最接近标准体重的学生体重是多少？
（2）求七名学生的平均体重；
（3）按体重的轻重排列时，恰好居中的是那个学生？
某工厂第一季度生产甲、乙两种机器共480台．改进生产技术后，计划第二季度生产这两种机器共554台，其中甲种机器产量要比第一季度增产10%，乙种机器产量要比第一季度增产20%．该厂第一季度生产甲、乙两种机器各多少台？
如图，若AD∥BC，∠A=∠D．
（1）猜想∠C与∠ABC的数量关系，并说明理由；
（2）若CD∥BE，∠D=50°，求∠EBC的度数．
小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：
| 项目 |
月功能费 |
基本话费 |
长途话费 |
短信费 |
| 金额/元 |
5 |
50 |
（1）请将表格补充完整；
（2）请将条形统计图补充完整；
（3）扇形统计图中，表示短信费的扇形的圆心角是多少度？
如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD．
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC；
（2）在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由．
）已知二元一次方程组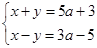
，其中x＜0，y＞0，求a的取值范围，并把解集在数轴上表示出来．