将函数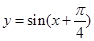
的图像向右平移
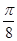，再把图像上所有点的横坐标缩短到原来的
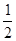纵坐标不变，则所得图像的解析式为（ ）
A． |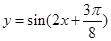
B． |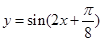
C． |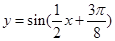
D． |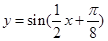
图1是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律放下去，至第七个叠放的图形中，小正方体木块总数就是（ ）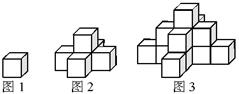
| A．25 | B．66 | C．91 | D．120 |
将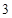
个不同的小球放入
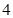个不同盒子中，则不同放法种数有（）
A． |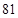
B． |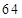
C． |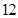
D． |
已知复数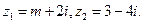
若
为实数，则实数m的值为（）
A． |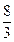
B． |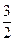
C． |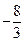
D． |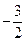
复数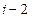
的虚部是（）
A． |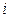
B． |
C．  |
D． |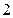
某同学做了一个如图所示的等腰直角三角形形状的数表且把奇数和偶数分别依次排在了数表的奇数行和偶数行，若用a(i，j)表示第 i行从左数第j个数，如a(4，3) = 10，
则a(21，6) = （）
| A．219 | B．211 | C．209 | D．213 |