如图所示,两个带等量异种电荷的点电荷,电荷量均为 Q,固定于同一条竖直线上的 A、B两点处, 其中 A处的电荷带正电,B处的电荷带负电,A、B相距为2 d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球 P,质量为 m、电荷量为+q (可视为点电荷),现将小球 P从与点电荷 A等高的 C 处由静止释放,小球 P 向下运动到与 C点距离为 d的 D 点时,速度为 v.已知 MN与 AB 之间的距离为 d,静电力常量为 k,重力加速度为 g,设取AB中点的电势为零,
试求:(1)在 A、B所形成的电场中 C点的电势 φC.
(2)小球 P 经过 D 点时的加速度.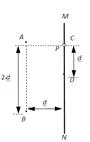
如图,在一个平面直角坐标系内,原点O处有一质点,质量为m。为使质点到达坐标为(d,d)的点P,现给质点施以大小为F的恒力,在起初的时间t1内该力方向为x轴正方向,之后的时间t2内该力变为y轴正方向,经过这两段运动质点刚好到达P点。试求:
(1)比值t1:t2;
(2)质点到达P点时的速度。
甲车停在平直公路上,乙车以速度v0=20m/s从甲车旁驶过,同时甲车启动开始追赶乙车。已知甲车的启动加速度为a=5m/s2,达到其最大速度v=30m/s后做匀速运动。试问:
(1)甲车追上乙车时是在加速阶段还是匀速阶段?
(2)甲车追上乙车一共所花的时间是多少?
如图半径分别为2R和R的甲、乙两光滑圆形轨道固定放置在同一竖直平面内,两轨道之间由一条水平轨道CD相连,曲面轨道与水平面轨道在B处光滑连接(物块经过B点时没有机械能损失),现有一小物块从斜面上高h处的A点由静止释放,曲面轨道以及水平轨道BC段是光滑的,小物块与CD段以及D右侧的水平轨道间的动摩擦因数均为μ。已知小物块通过甲轨道最高点时与轨道间压力为物块重力的3倍,而后经过有摩擦的CD段后又进入乙轨道运动。
(1)求初始释放物块的高度h
(2)为避免出现小物块脱离圆形轨道乙而发生撞轨现象,则CD段的长度应满足什么条件?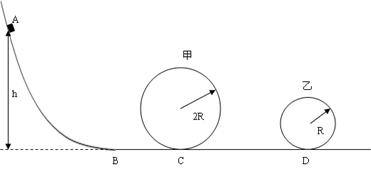
如图所示在光滑水平Oxy平面的ABCD区域内,小球在区域ABEO和MNCD水平方向均仅受到大小皆为F的水平恒力,在ABEO区域F力的方向沿X轴负方向,在MNCD区域F力的方向沿y轴负方向,在中间的DENM区域不受任何水平力的作用。两恒力区域的边界均是边长为L的正方形,即AO=OM=MD=DC=L,如图所示。
(1)在该区域AB边的中点处由静止释放一小球,求小球离开ABCD区域的位置坐标.
(2)在ABEO区域内适当位置由静止释放小球,小球恰能从ABCD区域左下角D处(即X轴上X=-2L处)离开,求所有释放点的位置坐标满足的关系。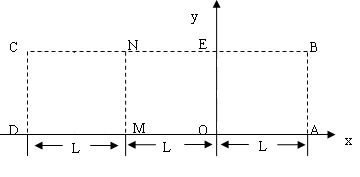
两个行星各有一个卫星绕其表面运行,已知两个卫星的周期之比为1∶3,两行星半径之比为3∶1 ,求:(1)两行星密度之比为多少?(2)两行星表面处重力加速度之比为多少?