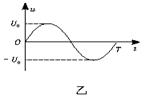
示波器是一种多功能电学仪器，可以在荧光屏上显示出被检测的电压波形。它的工作原理等效成下列情况：（如图所示）真空室中电极K发出电子（初速不计），经过电压为U1的加速电场后，由小孔S沿水平金属板，A、B间的中心线射入板中。板长L，相距为d，在两板间加上如图乙所示的正弦交变电压，周期为T，电压的最大值U0，前半个周期内B板的电势高于A板的电势，电场全部集中在两板之间，且分布均匀。在每个电子通过极板的极短时间内，电场视作恒定的。在两极板右侧且与极板右端相距D处有一个与两板中心线垂直的荧光屏（非常大），中心线正好与屏上坐标原点相交。当第一个电子到达坐标原点O时，使屏以速度v沿-x方向运动，每经过一定的时间后，在一个极短时间内它又跳回到初始位置，然后重新做同样的匀速运动。(已知电子的质量为m，带电量为e，不计电子重力)求：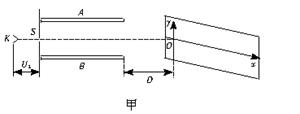
（1）电子进入AB板时的初速度；
（2）要使所有的电子都能打在荧光屏上，电压的最大值U0需满足什么条件？
（3）要使荧光屏上始终显示一个完整的波形，荧光屏必须每隔多长时间回到初始位置？计算这个波形的最大峰值和长度。
如图所示，电阻忽略不计的、两根平行的光滑金属导轨竖直放置，其上端接一阻值为3 Ω的定值电阻R. 在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B、磁场区域的高度为d="0.5" m. 导体棒a的质量ma="0.2" kg,电阻Ra="3" Ω；导体棒b的质量mb="0.l" kg，电阻Rb="6" Ω.它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动，且都能匀速穿过磁场区域，当b刚穿出磁场时a正好进入磁场. 设重力加速度为g="l0" m/s2. （不计a、b之间的作用，整个运动过程中a、b棒始终与金属导轨接触良好）求：
（1）在整个过程中，a、b两棒克服安培力分别做的功；
（2）a进入磁场的速度与b进入磁场的速度之比；
（3）分别求出M点和N点距L1的高度.
在如图所示的空间里，存在垂直纸面向里的匀强磁场，磁感应强度为
.在竖直方向存在交替变化的匀强电场如图（竖直向上为正），电场大小为
．一倾角为θ足够长的光滑绝缘斜面放置在此空间．斜面上有一质量为m，带电量为-q的小球，从t=0时刻由静止开始沿斜面下滑，设第5秒内小球不会离开斜面，重力加速度为g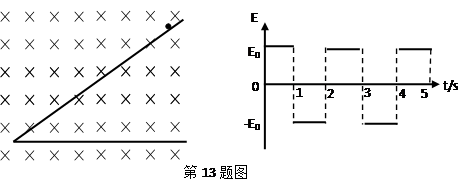
求：（1）求第1秒末小球的速度大小．
(2)第6秒内小球离开斜面的最大距离．
（3）若第19秒内小球仍未离开斜面，θ角应满足什么条件？
氢原子处于基态时，原子能量E1=－13.6eV，已知电子电量e，电子质量m，氢的核外电子的第一条可能轨道的半径为r1，已知氢原子各定态能量与基态能量之间关系为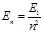
，式中n=2、3、4、5……
（1）氢原子核外电子的绕核运动可等效为一环形电流，处于基态的氢原子核外电子运动的等效电流多大？ （用k，e，r1，m表示）
（2）若氢原子处于n=2的定态，求该氢原子的电离能．
一束光波以450的入射角，从AB面射入如图所示的透明三棱镜中，棱镜折射率n=
．试求光进入AB面的折射角，并在图上画出该光束在棱镜中的光路图．
（1）如图所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体．活塞的质量为m，横截面积为S，与容器底部相距H．现通过电热丝缓慢加热气体，活塞逐渐上升，活塞与缸壁间摩擦不计．下列说法正确的是_______________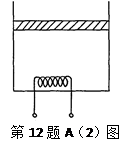
| A．上述过程气体做等压膨胀，温度升高 |
| B．上述过程气体做绝热膨胀，温度升高 |
| C．气体的吸收热量大于它对外做功，内能增加 |
| D．气体吸收的热量等于它对外做功，内能不变 |
（2）在上小题中，已知该理想气体摩尔质量为μ，在加热之前该气体的密度为ρ，阿伏加德罗常数为NA，求容器内理想气体的分子数n和加热之前分子间的平均距离d（忽略电热丝体积大小）．