(本小题满分12分)如图所示,四棱锥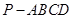 中,
中,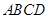 为正方形,
为正方形,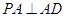
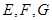 分别是线段
分别是线段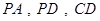 的中点. 求证:
的中点. 求证:
(1)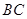 //平面
//平面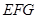 ;
;
(2)平面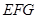 ⊥平面
⊥平面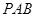 .
.
已知等差数列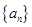 满足:
满足: ,
, ,
,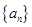 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)令bn= (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.
已知向量 ,函数
,函数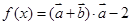 .
.
(1)求函数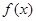 的最小正周期
的最小正周期 ;
;
(2)已知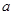 、
、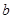 、
、 分别为
分别为 内角
内角 、
、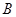 、
、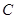 的对边, 其中
的对边, 其中 为锐角,
为锐角, ,且
,且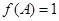 ,求
,求 和
和 的面积
的面积 .
.
如图,在底面为平行四边形的四棱锥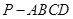 中,
中, 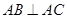 ,
,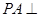 平面
平面 ,点
,点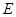 是
是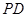 的中点.
的中点.
(1)求证: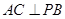 ;
;
(2)求证: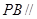 平面
平面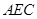 ;
;
已知函数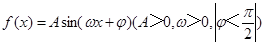 的图象在y轴上的截距为1,它在y轴右侧的第一个最高点和最低点分别为
的图象在y轴上的截距为1,它在y轴右侧的第一个最高点和最低点分别为 和
和
(1)求函数 的解析式;
的解析式;
(2)求函数f(x)的最小正周期和单调增区间.
(3)函数 的图像由
的图像由 怎样变换来的
怎样变换来的
(4)若 ,求函数y=f(x)的最大值和最小值以及取最值时对应的x的值
,求函数y=f(x)的最大值和最小值以及取最值时对应的x的值
平面内给定三个向量 ,
, ,
, ,回答下列问题
,回答下列问题
(1)求满足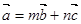 的实数
的实数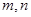
(2)若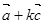 ∥
∥ ,求实数
,求实数