如图所示，固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷，电荷量均为Q，其中A带正电荷，B带负电荷，A、B相距为2d。MN是竖直放置的光滑绝缘细杆，另有一个穿过细杆的带电小球P，质量为m、电荷量为+q(可视为点电荷)，现将小球P从与点电荷A等高的C处由静止开始释放，小球P向下运动到距C点距离为d的D点时，速度为v。已知MN与AB之间的距离为d，静电力常量为k，重力加速度为g，若取无限远处的电势为零，试求：
(1)在A、B所形成的电场中，C的电势φC。
(2)小球P经过D点时的加速度。
如图所示，一质量为0.5kg的小球，用0.4m长的细线拴住在竖直面内作圆周运动，求(1)小球在圆周上最高点速度为4m/s时，细线的拉力是多少？(2)小球在圆上最低点速度为4
m/s时，细线的拉力又是多少？(3) 要使小球通过最高点处时细线对球无作用力，此时小球在最高点处速度为多少？（g=10m/s2）
如图所示，在高15m的平台上，有一个小球被细线拴在墙上，球与墙之间有一被压缩的轻弹簧，当细线被烧断时，小球被弹出，不计一切阻力，（1）小球在空中运动的时间是多少？（2）已知小球落地时速度方向与水平成60°角，求小球被弹簧弹出时的速度大小？(3)小球落地时小球在水平方向的位移多大？(
)
在距离地面足够高的某处，以30m/s的初速度竖直向上抛出一小球，不计空气阻力的作用。求（1）8s末小球的速度大小和方向。（2）8s内小球的位移大小和方向。（3）8s内小球通过的路程是多大。（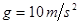
）
某天体的半径为地球半径的4倍，质量为地球质量的16倍，已知地球的第一宇宙速度为7.9Km/s,则该天体的第一宇宙速度的大小为多少?
一车处于静止状态，车后相距s0=25m处有一个人，当车开始启动以1m/s2的加速度前进的同时，人以6m/s速度匀速追车，能否追上？若追不上，人车间最小距离为多少？