（本题14分）下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（
吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
|
3 |
4 |
5 |
6 |
|
2.5 |
3 |
4 |
4.5 |
（1）请画出上表数据的散点图；并指出x，y 是否线性相关；
（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（3）已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考:用最小二乘法求线性回归方程系数公式 
，
）
已知函数
是奇函数.
(1)求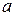
的值;
(2)判断函数
的单调性,并用定义证明;
(3)求函数的值域.
已知集合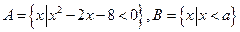 
.
(1)若
,求实数
的取值范围；
(2)若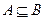
,求实数的取值范围.
已知函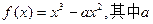数
为正常数。
（1）设当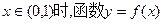
图象上任一点P处的切线的斜率为k，若
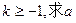的取值范围；
（2）当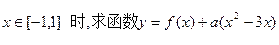
的最大值。
（（本小题满分14分）已知圆O：
直线
。
（I）求圆O上的点到直线
的最小距离。
|
（II）设圆O与
轴的两交点是F1、F2，若从F1发出的光线经上的点M反射后过点F2，求以F1、F2为焦点且经过点M的椭圆方程。
已知圆C经过P（4，– 2），Q（– 1，3）两点，且在y轴上截得的线段长为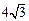
，半径小于5．
（1）求直线PQ与圆C的方程．
（2）若直线l∥PQ，且l与圆C交于点A、B，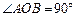
，求直线l的方程．