如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系.设该圆弧所在圆的圆心为点D,连结AD、CD.
请完成下列问题:
(1)出点D的坐标:D___________;
(2)D的半径=_____(结果保留根号);
(3)若扇形DAC是一个圆锥的侧面展开图,则该圆锥的底面面积为__________(结果保留π);
(4)若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
计算: -2
-2 +sin260°+cos260°.
+sin260°+cos260°.
如图,已知:⊙D交y轴于A、B,交x轴于C,过点C的直线:y=-2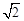 -8 与y轴交于点P.
-8 与y轴交于点P.
(1)试判断PC与⊙D的位置关系.
(2)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由。
如图,AB为半圆O的直径,在AB的同侧作AC、BD切半圆O于A、B,CD切半圆O于E,请分别写出两个角相等、两条边相等、两个三角形全等、两个三角形相似等四个正确的结论.
如图,有三边分别为0.4m、0.5m和0.6m的三角形形状的铝皮,问怎样剪出一个面积最大的圆形铝皮?请你设计解决问题的方法.
如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.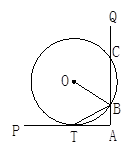
(1)BT是否平分∠OBA?证明你的结论.
(2)若已知AT=4,试求AB的长.