当人造地球卫星的运行速度大于第一宇宙速度而小于第二宇宙速度时,它能环绕地球运行,已知第一宇宙速度的公式是v1=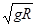 (米/秒),第二宇宙速度的公式是v2=
(米/秒),第二宇宙速度的公式是v2=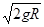 (米/秒),其中g=9.8米/秒,R=6.4×106米.试求第一、第二宇宙速度(结果保留两个有效数字).
(米/秒),其中g=9.8米/秒,R=6.4×106米.试求第一、第二宇宙速度(结果保留两个有效数字).
(本题10分)用你发现的规律解答下列问题.

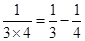 ┅┅
┅┅
(1) 计算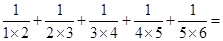 .
.
(2)探究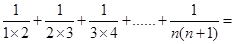 .(用含有
.(用含有 的式子表示)
的式子表示)
(3)若 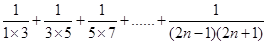 的值为
的值为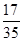 ,求
,求 的值.
的值.
(本题9分)为了了解“通话时长”(“通话时长”指每次通话时间)的分布情况,小强收集了他家1000个“通话时长”数据,这些数据均不超过18(单位:分钟),他从中随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完成的频数分布直方图.
| “通话时长” x/分钟 |
0<x≤3 |
3<x≤6 |
6<x≤9 |
9<x≤12 |
12<x≤15 |
15<x≤18 |
| 次数 |
36 |
a |
8 |
12 |
8 |
12 |
|
根据图、表提供的信息,解答下列问题:
(1)a= ,样本容量是 ,并将这个频数分布直方图补充完整;
|
(2)求样本中“通话时长”不超过9分钟的频率;
(3)请估计小强家这1000次通话中“通话时长”超过15分钟的次数.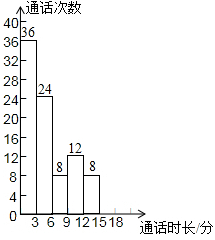
(本题6分)如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图并标好相应的字母: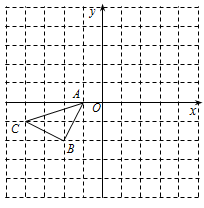
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转 得△AB1C1,画出△AB1C1.
得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(本题6分)如图,在□ABCD中,点E,F是对角线BD上的两点,且BE=DF.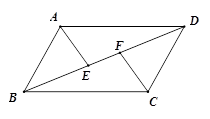
求证:(1)△ABE≌△CDF;(2)AE∥CF.
(本题8分)(1)计算:(1+ )÷
)÷
(2)解方程: +
+ =-1
=-1