已知X光子的能量为0.6 MeV,在康普顿散射后,波长变化了20%,求反冲电子的能量.
(12分)如图所示电路中,己知电源电动势E=12V内电阻r=1.0Ω,电阻R1=9.0Ω、R2=15Ω、R3=30Ω.(不计电流表的内阻)求: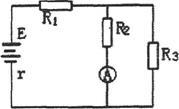
(1)电流表A示数;
(2)电阻R3消耗的电功率.
A、B两车在同一直线上向右匀速运动,B车在A车前,A车的速度大小为V1=8m/s, B车的速度大小为V2=20m/s,如图所示。当A、B两车相距x0=28m时,B车因前方突发情况紧急刹车(已知刹车过程的运动可视为匀减速直线运动),加速度大小为a=2m/s2,从此时开始计时,求:
(1)B车减速到与A车速度相等时所用的时间和前进的位移;
(2)A车追上B车之前,两者相距的最大距离;
(3)A车追上B车所用的时间;
(4)从安全行驶的角度考虑,为避免两车相撞,在题设条件下,A车在B车刹车的同时也应刹车的最小加速度.
如图所示,光滑金属球的重力G=40 N.它的左侧紧靠竖直的墙壁,右侧置于倾角θ=37°的斜面体上。已知斜面体处于水平地面上保持静止状态,sin 37°=0.6,cos 37°=0.8.求:
(1)金属球对墙壁和斜面的弹力大小;
(2)水平地面对斜面体的摩擦力的大小和方向
如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m。直杆位于 圆筒正上方H=0.8m处。直杆从静止开始做自由落体运动,并能竖直穿越圆筒。(取g=10m/s2),试求:(1)直杆下端刚到圆筒上端的时间;(2)直杆穿越圆筒所用的时间。
如图所示,木板A的质量为m="0.1" kg,滑块B的质量为M="0.3" kg,木板A用绳拴住,绳与斜面平行,B恰好能沿倾角为θ=370的斜面在A木板下向下滑动.A、B间以及B与斜面间的动摩擦因数相同都为μ=0.2,sin370=0.6,cos370=0.8,g=10m/s2,求:
(1)作出B物体受力分析图;
(2)A对B的压力?B对斜面的压力?
(3)B物体所受摩擦力.