小明、小亮、小梅、小花四人共同探究代数式x2-4x+5的值的情况，他们作了如下分工：小明负责找值为1时的x值，小亮负责找值为0时的x值，小梅负责找最小值，小花负责找最大值。几分钟后，各自通报探究的结论，其中错误的是（ ）
| A．小明认为只有当x=2时，x2-4x+5的值为1； |
| B．小亮认为找不到实数x，使x2-4x+5的值为0； |
| C．小花发现当取大于2的实数时，x2-4x+5的值随x的增大而增大，因此认为没有最大值； |
| D．小梅发现x2-4x+5的值随x的变化而变化，因此认为没有最小值； |
一个几何体如图所示，则该几何体的三视图正确的是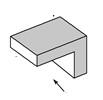
下列图形中，是中心对称图形但不是轴对称图形的是（）
A． |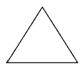
B． |
C． |
D． |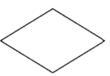
在实数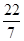
，
，
，
，
，
，
，
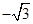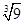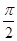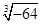中，无理数有（）．
| A．1个 | B．2个 | C．3个 | D．4个 |
二次函数y＝ax2＋bx＋c（a≠0）的部分图象如图所示，图象过点（－1，0），对称轴为直线x＝2．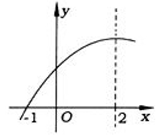
下列结论：
①4a＋b＝0；
②9a＋c＞3b；
③8a＋7b＋2c＞0；
④当x＞－1时，y的值随x值的增大而增大．
其中正确的结论有（）
| A．1个 | B．2个 | C．3个 | D．4个 |
【改编】如图，A、B是函数y=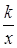
(k>0)的图像上关于原点对称的任意两点，BC∥x轴，AC∥y轴，S△ABC=4，则k=（）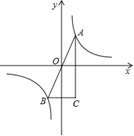
A．2 B．4 C．6 D．8