如图,已知□ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:四边形GEHF是平行四边形.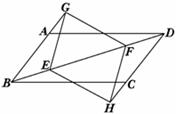
根据条件求下列抛物线的解析式:
(1)二次函数的图象经过(0,1),(2,1)和(3,4);
(2)抛物线的顶点坐标是(﹣2,1),且经过点(1,﹣2).
如图,二次函数y=ax2+bx+c的图象过A、B、C三点.
(1)求出抛物线解析式和顶点坐标;
(2)当﹣2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
如图为抛物线y=﹣x2+bx+c的一部分,它经过A(﹣1,0),B(0,3)两点.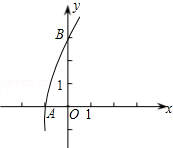
(1)求抛物线的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
一个二次函数的图象经过点(0,0),(﹣1,﹣1),(1,9)三点,求这个函数的关系式.
已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).求二次函数的解析式.