实验室里的交流发电机可简化为如图所示的模型,正方形线圈在水平匀强磁场中,绕垂直于磁感线的OO′轴匀速转动.今在发电机的输出端接一个电阻R和理想电压表,并让线圈每秒转25圈,读出电压表的示数为10 V.已知R=10 Ω,线圈电阻忽略不计,下列说法正确的是 ( )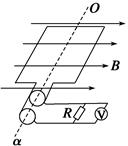
A.线圈平面与磁场平行时刻,线圈中的瞬时电流为零
B.从线圈平面与磁场平行开始计时,线圈中感应电流瞬时值表达式为i=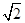 sin 100πt (A)
sin 100πt (A)
C.流过电阻R的电流最大值为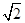 A
A
D.电阻R上的热功率等于5 W
关于波动,下列说法正确的是( )
| A.各种波均会发生偏振现象 |
| B.用白光做单缝衍射与双缝干涉实验,均可看到彩色条纹 |
| C.声波传播过程中,介质中质点的运动速度等于声波的传播速度 |
| D.已知地震波的纵波波速大于横波波速,此性质可用于横波的预警 |
在一次讨论中,老师问道:“假如水中相同深度处有a、b、c三种不同颜色的单色点光源,有人在水面上方同等条件下观测发现,b 在水下的像最深,c照亮水面的面积比a的大.关于这三种光在水中的性质,同学们能做出什么判断?”有同学回答如下:
①c光的频率最大 ②a光的传播速度最小 ③b光的折射率最大 ④a光的波长比b光的短
根据老师的假定,以上回答正确的是( )
| A.①② | B.①③ | C.②④ | D.③④ |
一列简谐横波在t=0时的波形图如图所示.介质中x=2 m处的质点P沿y轴方向做简谐运动的表达式为y=10 sin(5πt)cm.关于这列简谐波,下列说法正确的是( )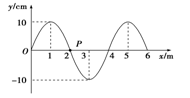
| A.周期为4.0 s |
| B.振幅为20 cm |
| C.传播方向沿x轴正向 |
| D.传播速度为10 m/s |
如图所示,水平粗糙地面上的物体被绕过光滑定滑轮的轻绳系着,现以大小恒定的拉力F拉绳的另一端,使物体从A点起由静止开始运动。若从A点运动至B点和从B点运动至C点的过程中拉力F做的功分别为W1、W2,若图中AB=BC,且动摩擦因数处处相同,则在物体的运动过程中,有:
A.摩擦力增大, |
B.摩擦力减小,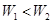 |
C.摩擦力增大,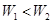 |
D.摩擦力减小, |
如图所示,用线把小球A悬于O点,静止时恰好与另一固定小球B接触。今使两球带同种电荷,悬线将偏离竖直方向某一角度θ1,此时悬线中的张力大小为T1;若增加两球的带电量,悬线偏离竖直方向的角度将增大为θ2,此时悬线中的张力大小为T2,则: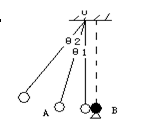
| A.T1<T2 | B.T1=T2 | C.T1>T2 | D.无法确定 |