如图a，间距为d的平行金属板MN与一对光滑的平行导轨相连，平行导轨间距L=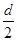
，一根导体棒ab以一定的初速度向右匀速运动，棒的右端存在一个垂直纸面向里，磁感应强度大小为B的匀强磁场。棒进入磁场的同时，粒子源P释放一个初速度为零的带电粒子，已知带电粒子质量为m，电荷量为q，粒子能从N板加速到M板，并从M板上的一个小孔穿出。在板的上方，有一个环形区域内存在磁感应强度大小也为B，垂直纸面向外的匀强磁场。已知外圆半径为2d，内圆半径为d，两圆的圆心与小孔重合(粒子重力不计)。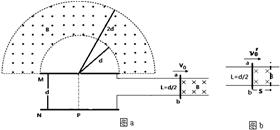
(1)判断带电粒子的正负，并求当ab棒的速度为vo时，粒子到达M板的速度v；
(2)若要求粒子不能从外圆边界飞出，则ab棒运动速度v0的取值范围是多少？
(3)若棒ab的速度
，为使粒子不从外圆飞出，可通过控制导轨区域磁场的宽度S(如图b)，则该磁场宽度S应控制在多少范围内？
如图所示，物体A放在足够长的木板B上，木板B静止于水平面。t=0时，电动机通过水平细绳以恒力F拉木板B，使它做初速度为零，加速度aB=1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数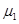
=0.05，B与水平面之间的动摩擦因数
=0.1，最大静摩擦力与滑动摩擦力大小视为相等，重力加速度g取10m/s2。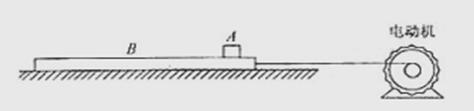
求（1）物体A刚运动时的加速度aA
（2）t=1.0s时，电动机的输出功率P；
（3）若t=1.0s时，将电动机的输出功率立即调整为P/=5W，并在以后的运动过程中始终保持这一功率不变，t=3.8s时物体A的速度为1.2m/s。则在t=1.0s到t=3.8s这段时间内木板B的位移为多少？
如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6 m/s的速度运动，运动方向如图所示．一个质量为2 kg的物体(物体可以视为质点)，从h＝3.2 m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失．物体与传送带间的动摩擦因数为0.5，物体向左最多能滑到传送带左右两端AB的中点处，重力加速度g＝10 m/s2，则：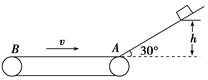
(1)物体由静止沿斜面下滑到斜面末端需要多长时间？
(2)传送带左右两端AB间的距离l至少为多少？
(3)上述过程中物体与传送带组成的系统产生的摩擦热为多少？
我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成。物理老师要求同学用所学的知识，设计一个测量月球密度的方案，交给我国将来登月的宇航员来完成。某研究小组提出如下方案：我们现已知万有引力常数G和月球的半径R，假设月球为密度均匀的球体。只要让宇航员在月球表面上从H高度自由释放一个小球，求出它下落的时间t , 就可求出月球的密度，请你求出该小组用上述已知量和假想的实验量来表示月球密度的表达式。
以速度为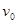
＝10m/s匀速行驶的汽车在第2s末关闭发动机，以后作匀减速直线运动，第3s内的平均速度是9m/s，试求：
（1）汽车作减速直线运动的加速度a；
（2）汽车在10s内的位移S。
(10分)A物体做匀速直线运动，速度是1m/s，A出发后5s，B物体从同一地点从静止开始出发做匀加速直线运动，加速度是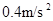
，且A、B运动方向相同，问：
⑴ B出发后几秒钟才能追上A？
⑵ A、B相遇前它们之间的最大距离是多少？