如图,MN是负点电荷电场中的一条电场线,一带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是:( )
| A.带电粒子在a点时的加速度小于于在b点时的加速度 |
| B.带电粒子在a点时的电势能大于在b点时的电势能 |
| C.带电粒子从a到b运动的过程中动能逐渐减小 |
| D.负点电荷一定位于N点右侧 |
如图所示,理想变压器原、副线圈的匝数比为10:1,电压表和电流表均为理想交流电表,从某时刻开始在原线圈两端加上交变电压,其瞬时值表达式为 ,则
,则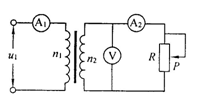 ()
()
A.电压表的示数为 |
| B.在滑动变阻器触头P向上移动的过程中,电流表A2的示数变小 |
| C.在滑动变阻器触头P向上移动的过程中,电流表A1的示数变大 |
| D.在滑动变阻器触头P向上移动的过程中,理想变压器的输入功率变小 |
如图所示,AB为斜面,BC为水平面,从A点以水平初速度v向右抛出一小球,其落点与A的水平距离为s1,从A点以水平初速度2v向右抛出一小球,其落点与A的水 平距离为s2,不计空气阻力,s1∶s2可能为( )
平距离为s2,不计空气阻力,s1∶s2可能为( )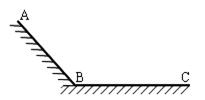
| A.1∶2 | B.1∶3 | C.1∶4 | D.1∶5 |
完全相同的直角三角形滑块A、B,按如图2-3-27所示叠放,设A、B接触的斜面光滑,A与桌面间的动摩擦因数为μ,现在B上作用一水平推力F,恰好使A、B一起在桌面上匀速运动,且A、B保持相对静止.则A与桌面间的动摩擦因数μ与斜面倾角θ的关系为( )
A.μ=tanθ /2 B.μ=tanθ C.μ=2tanθ D.μ与θ无关
被竖直上抛的物体,抛出时的初速度与回到抛出点时的速度大小之比为R,设空气阻力在运动中大小不变。则重力与空气阻力大小之比为( )
A.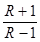 |
B.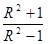 |
C.R2 | D.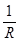 |
如图所示的位移(s)—时间(t)图象和速度(v)—时间(t)图象中,给出四条曲线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是()
| A.图线1表示物体做曲线运动 |
| B.s—t图象中t1时刻v1>v2 |
| C.v—t图象中0至t3时间内3和4的平均速度大小相等 |
| D.两图象中,t2、t4时刻分别表示2、4开始反向运动 |