如图所示,在x-o-y坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场的磁感应强度大小为B,方向垂直于纸面向里。在y > r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E。从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r。已知质子的电荷量为q,质量为m,不计质子所受重力及质子间相互作用力的影响。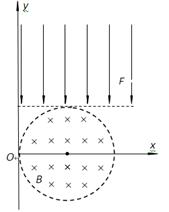
(1)求质子射入磁场时速度的大小;
(2)若质子沿x轴正方向射入磁场,求质子从O点进入磁
场到第二次离开磁场经历的时间;
如图11-2-13所示,一圆柱形容器竖直放置,通过活塞封闭着摄氏温度为t的理想气体.活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝给气体加热一段时间,结果活塞缓慢上升了h,若这段时间内气体吸收的热量为Q,已知大气压强为p0,重力加速度为g,不计器壁向外散失的热量及活塞与器壁间的摩擦,求:
(1)气体的压强;
(2)这段时间内气体的内能增加了多少?
(3)这段时间内气体的温度升高了多少?
有人设计了一种测温装置,其结构如图11-2-12所示.玻璃泡A内封有一定量气体,与管A相连的B管插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出.设B管的体积与A泡的体积相比可略去不计.
(1)B管刻度线是在1标准大气压下制作的(1标准大气压相当于76
cm水银柱的压强).已知当温度t=27℃时的刻度线在x=16 cm处,
问t=0℃的刻度线在x为多少厘米处?
(2)若大气压已变为相当于75 cm水银柱的压强,利用该测温装置测量温度时所得读数
仍为27℃,问此时实际温度为多少?
如图11-2-11所示,粗细均匀的弯曲玻璃管A、B两端开口.管内有一段水银柱,右管内气柱长为39 cm,中管内水银面与管口A之间气柱长为40 cm.先将B端封闭,再将左管竖直插入水银槽,设整个过程温度不变,稳定后右管内水银面比中管内水银面高 2 cm.求:
(1)稳定后右管内的气体压强p;
(2)左管A端插入水银槽的深度h.(大气压强p0=76 cmHg)
某同学在夏天游玩时,看到有一些小昆虫可以在水面上停留或能跑来跑去而不会沉入水中,尤其是湖水中鱼儿戏水时吐出小气泡的情景,觉得很美,于是画了一幅鱼儿戏水的图画如图11-2-10所示.但旁边的同学考虑到上层水温较高和压强较小的情况,认为他的画有不符合物理规律之处,请根据你所掌握的物理知识指出正确的画法(用简单的文字表述,不要画图),并指出这样画的物理依据.
(1)正确的画法应为:__________________________.
(2)物理学依据:____________________________.
(3)试分析小昆虫在水面上不会沉入水中的原因________________________________.
一定质量的理想气体由状态A经状态B变为状态C,其中A→B过程为等压变化,B→C过程为等容变化.已知VA=0.3 m3,TA=TC=300 K,TB=400 K.
(1)求气体在状态B时的体积.
(2)说明B→C过程压强变化的微观原因.
(3)设A→B过程气体吸收热量为Q1,B→C过程气体放出热量为Q2,比较Q1、Q2的大小并说明原因.