已知点 是抛物线
是抛物线
 上一点,
上一点, 为抛物线的焦点,准线
为抛物线的焦点,准线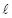 与
与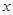 轴交于点
轴交于点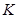 ,已知
,已知 =
=
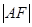 ,三角形
,三角形 的面积等于8.
的面积等于8.
(1)求 的值;
的值;
(2)过该抛物线的焦点作两条互相垂直的直线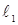 ,
,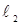 ,与抛物线相交得两条弦,两条弦的中点分别为
,与抛物线相交得两条弦,两条弦的中点分别为 .求
.求 的最小值.
的最小值.
如图所示,流程图给出了无穷等差整数列 ,
, 时,输出的
时,输出的 时,输出的
时,输出的 (其中d为公差)
(其中d为公差)
(I)求数列 的通项公式;
的通项公式;
(II)是否存在最小的正数m,使得 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。
已知
(1)求使 上是减函数的充要条件;
上是减函数的充要条件;
(2)求 上的最大值。
上的最大值。
AB为圆O的直径,点E、F在圆上,AB//EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1。
(I)求证:BF⊥平面DAF;
(II)求ABCD与平面CDEF所成锐二面角的某三角函数值;
(III)求多面体ABCDFE的体积。
甲、乙两个同学同时报名参加某重点高校2010年自主招生,高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格。已知甲,乙两人审核过关的概率分别为 ,审核过关后,甲、乙两人文化测试合格的概率分别为
,审核过关后,甲、乙两人文化测试合格的概率分别为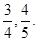
(1)求甲,乙两人至少有一人通过审核的概率;
(2)设 表示甲,乙两人中获得自主招生入选资格的人数,求
表示甲,乙两人中获得自主招生入选资格的人数,求 的数学期望.
的数学期望.
已知函数
(1)若 的最大值和最小值;
的最大值和最小值;
(2)若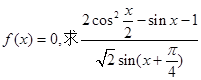 的值。
的值。