(本小题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段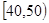 ,
, …
… 后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
(1)求第四小组 的频率.
的频率.
(2)求样本的众数.
(3) 观察频率分布直方图图形的信息,估计这次考试的及格率(60分及以上为及格)和平均分.
(本小题满分12分)
己知圆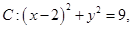 直线
直线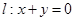 .
.
(1) 求与圆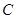 相切, 且与直线
相切, 且与直线 平行的直线
平行的直线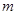 的方程;
的方程;
(2) 若直线 与圆
与圆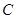 有公共点,且与直线
有公共点,且与直线 垂直,求直线
垂直,求直线 在
在 轴上的截距
轴上的截距 的取值范围.
的取值范围.
(本小题满分12分)
计算下列各式:
(1) ;
;
(2)
 .
.
(本小题满分13分)
已知点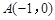 ,
,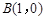 ,△
,△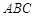 的周长为6.
的周长为6.
(Ⅰ)求动点 的轨迹
的轨迹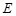 的方程;
的方程;
(Ⅱ)设过点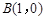 的直线
的直线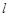 与曲线
与曲线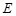 相交于不同的两点
相交于不同的两点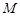 ,
, .若点
.若点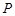 在
在 轴上,且
轴上,且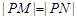 ,求点
,求点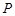 的纵坐标的取值范围.
的纵坐标的取值范围.
(本小题满分13分)
如图,在四棱锥 中,底面
中,底面 是正方形.已知
是正方形.已知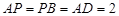 ,
, .
.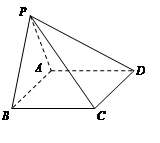
(Ⅰ)求证: ;
;
(Ⅱ)求四棱锥 的体积
的体积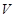 .
.
(本小题满分12分)
已知⊙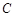 的圆心
的圆心 ,被
,被 轴截得的弦长为
轴截得的弦长为 .
.
(Ⅰ)求圆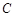 的方程;
的方程;
(Ⅱ)若圆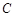 与直线
与直线 交于
交于 ,
, 两点,且
两点,且 ,求
,求 的值.
的值.