如图所示，水平放置的平行金属板A和D间的距离为d，金属板长为
，两板间所加电压为U，D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K，NM与水平挡板NP成
角，且挡板足够长，K与N间的距离为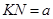
.现有一质量为m、电荷量为q的带正电的粒子，从A、D的中点O沿平行于金属板方向
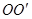以某一速度射入，不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K：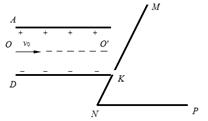
（1）求该粒子从O点射入时的速度大小v0；
（2）若两档板所夹的整个区域存在一垂直纸面向外的匀强磁场，粒子经过磁场偏转后能垂直打在水平挡板NP上，求该磁场的磁感应强度的大小B0；
（3）若磁场方向变为垂直纸面向里，且只存在于两档板所夹间的某一区域内，同样使该粒子经过磁场偏转后能垂直打在水平挡板NP上（之前与挡板没有碰撞），求满足条件的磁感应强度的最小值Bmin.
如图是一列简谐波在t =0时的波动图象，波的传播速度为2m/s，则从t=0到t=2.5s的时间内，质点M通过的路程是多少？t=2.5s时刻M点对平衡位置的位移是多少？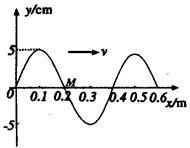
如图所示，在边长为a的正方形ABCD的对角线AC左右两侧，分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场， AD、CD是两块固定荧光屏（能吸收打到屏上的粒子）。现有一群质量为m、电量为q的带正电粒子，从A点沿AB方向以不同速率连续不断地射入匀强磁场中，带电粒子速率范围为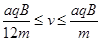 
。已知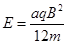
，不计带电粒子的重力和粒子之间的相互作用。求：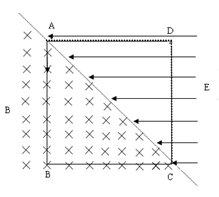
（1）恰能打到荧光屏C D上的带电粒子的入射速度；
（2）AD、CD两块荧光屏上形成亮线的长度。
如图所示，电源电动势E＝6 V，内阻r＝1 Ω，电阻R1＝2 Ω，R2＝3 Ω，R3＝7.5 Ω，电容器的电容C＝4 μF.开关S原来断开，现在合上开关S到电路稳定，试问这一过程中通过电流表的电荷量是多少？
如图所示，已知电阻R1=4.0Ω，R2=6.0Ω，电源内阻r=0.60Ω，电源的总功率P总=40W，电源输出功率P出=37.6W。求：
⑴A、B间的电压U；
⑵电源电动势E；
⑶R3的阻值。
磁强计是一种测量磁感应强度的仪器，其原理如图所示，电路中有一段金属导体，它的横截面是宽为a ，高为b的长方形，放在沿y轴正方向的匀强磁场中，导体中通有沿x轴正方向、电流强度为I的电流。已知导体中单位体积的自由电子数为n ，电子电量为e 。测出导体前后两个侧面的电势差为U 。
⑴导体前后两个侧面哪个面电势较高？
⑵磁感应强度B的大小为多大？