如图所示,竖直放置、宽度L=1.0m的框架上,放有一质量m=0.1kg、电阻R=1.0Ω的导体棒MN,它们处于磁感应强度B=1.0T的匀强磁场中,磁场方向与框架平面垂直。用电动机无初速牵引导体棒上升,当上升到h=3.8m时,获得稳定的速度,导体棒上产生的热量Q=2.0J,电动机牵引棒时,电压表、电流表的读数分别为U=7.0V、I=1.0A,电动机内阻r=1.0Ω。不计其它电阻及一切摩擦,导体棒与框架始终接触良好,取重力加速度g=10 m/s2 。求: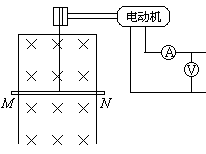
(1)棒能达到的稳定速度的大小v;
(2)棒从静止至达到稳定速度所需要的时间t。
如图所示,在同一竖直平面内有A、B两物体,A物体从a点起以角速度 做半径为R的匀速圆周运动,同时B物体从圆心O点处自由下落,若要A、B两物体在d点相遇,求角速度
做半径为R的匀速圆周运动,同时B物体从圆心O点处自由下落,若要A、B两物体在d点相遇,求角速度 须满足的条件。
须满足的条件。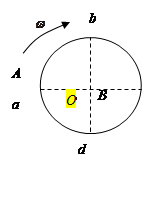
城市中为了解决交通问题,修建了许多立交桥,如图所示,桥面为圆弧形的立交桥AB,横跨在水平路面上,长L=200m,桥高20m。可认为桥的两端A、B与水平路面的连接处是平滑的。一辆小汽车的质量m=1040kg,以25m/s的速度冲上此立交桥,假设小汽车冲上立交桥后就关闭了发动机,不计车受到的阻力。求(1)小汽车冲上桥顶时的速度多大?(2)小汽车在桥顶处对桥面的压力多大?(g取10m/s2)
如图所示,在倾角为 的斜面上,一物块通过轻绳牵拉压紧弹簧。现将轻绳烧断,物块被弹出,与弹簧分离后即进入足够长的
的斜面上,一物块通过轻绳牵拉压紧弹簧。现将轻绳烧断,物块被弹出,与弹簧分离后即进入足够长的 粗糙斜面(此前摩擦不计),沿斜面上滑达到最远点位置离N距离为s。此后下滑,第一次回到N处,压缩弹簧后又被弹离,第二次上滑最远位置离N距离为
粗糙斜面(此前摩擦不计),沿斜面上滑达到最远点位置离N距离为s。此后下滑,第一次回到N处,压缩弹簧后又被弹离,第二次上滑最远位置离N距离为 。求:
。求:
(1)物块与粗糙斜面间的动摩擦因数;
(2)物体最终克服摩擦力做功所通过的总路程。
质量为1kg的物体以36m/s的初速度竖直上抛,经2s后速度减小为12m/s,在此过程中空气阻力大小不变。求:
(1)物体增加的重力势能
(2)物体克服阻力所做的功
用如图甲所示的滑轮组提升水中的物体M1,动滑轮A所受重力为G1,物体M1完全在水面下以速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为F1,拉力F1做功的功率为P1,滑轮组的机械效率为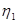 ;为了提高滑轮组的机械效率,用所受重力为G2的动滑轮B替换动滑轮A,如图乙所示,用替换动滑轮后的滑轮组提升水中的物体M2,物体M2完全在水面下以相同的速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为F2,拉力F2做功的功率为P2,滑轮组的机械效率为
;为了提高滑轮组的机械效率,用所受重力为G2的动滑轮B替换动滑轮A,如图乙所示,用替换动滑轮后的滑轮组提升水中的物体M2,物体M2完全在水面下以相同的速度v匀速竖直上升的过程中,卷扬机加在绳子自由端的拉力为F2,拉力F2做功的功率为P2,滑轮组的机械效率为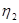 。已知:G1-G2=30N,
。已知:G1-G2=30N,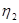 -
-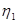 =5%,
=5%,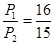 ,M1、M2两物体的质量相等,体积V均为4×10-2m3,g取10N/kg,绳重、轮与轴的摩擦及水的阻力均可忽略不计。
,M1、M2两物体的质量相等,体积V均为4×10-2m3,g取10N/kg,绳重、轮与轴的摩擦及水的阻力均可忽略不计。
求:(1)物体M1受到的浮力F浮;
(2)拉力F1与F2之比;
(3)物体M1受到的重力G。