(本小题满分12分)已知函数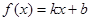 的图象与
的图象与 轴分别相交于点
轴分别相交于点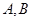 ,
, 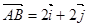 (
(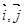 分别是与
分别是与 轴正半轴同方向的单位向量),函数
轴正半轴同方向的单位向量),函数 .
.
(1)求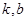 的值;
的值;
(2)当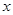 满足
满足 时,求函数
时,求函数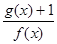 的最小值.
的最小值.
已知圆k过定点A(a,0)(a>0),圆心k在抛物线C: y2=2ax上运动,MN为圆k在y轴上截得的弦.
(1)试问MN的长是否随圆心k的运动而变化?
(2)当|OA|是|OM|与|ON|的等差中项时,抛物线C的准线与圆k有怎样的位置关系?
已知双曲线C的两条渐近线都过原点,且都以点A(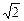 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
(1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为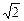 ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标.
已知直线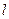 过定点A(4,0)且与抛物线
过定点A(4,0)且与抛物线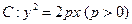 交于P、Q两点,若以PQ为直径的圆恒过原点O,求
交于P、Q两点,若以PQ为直径的圆恒过原点O,求 的值。
的值。
试确定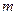 的取值范围,使得椭圆
的取值范围,使得椭圆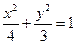 上有不同两点关于直线
上有不同两点关于直线 对称.
对称.
若抛物线 上总存在关于直线
上总存在关于直线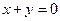 对称的两点,求
对称的两点,求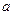 的范围.
的范围.