(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| |
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为 ,其中
,其中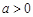 ,
,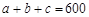 。当数据
。当数据 的方差
的方差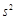 最大时,写出
最大时,写出 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时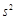 的值.
的值.
(注: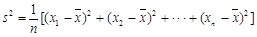 ,其中
,其中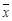 为数据
为数据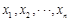 的平均数)
的平均数)
 ,
, ,求(1)
,求(1) (2)
(2)
(本小题满分14分)
已知数列{an}中,a1=t(t∈R,且t≠0,1),a2=t2,且当x=t时,
函数f(x)=(an-an-1)x2-(an+1-an)x(n≥2,n∈N)取得极值.
(Ⅰ)求证:数列{an+1-an}是等比数列;
(Ⅱ)若bn=anln|an|(n∈N),求数列{bn}的前n项和Sn;
(Ⅲ)当t=-时,数列{bn}中是否存在最大项?如果存在,说明是第几项;如果不存在,请说明理由.
(本小题满分14分)
已知F1,F2分别是椭圆+=1的左、右焦点,曲线C是以坐标原点为顶点,以F2为焦点的抛物线,自点F1引直线交曲线C于P、Q两个不同的交点,点P关于x轴的对称点记为M.设=λ.
(Ⅰ)求曲线C的方程;
(Ⅱ)证明:=-λ;
(Ⅲ)若λ∈[2,3],求|PQ|的取值范围.
(本小题满分13分)
设定义在R上的函数f(x)=a0x4+a1x3+a2x2+a3x+a4(a0,a1,a2,a3,a4∈R)当x=-1时,f(x)取得极大值,且函数y=f(x+1)的图象关于点(-1,0)对称.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)试在函数y=f(x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-,]上;
(Ⅲ)设xn=,ym=(m,n∈N),求证:|f(xn)-f(ym)|<.
(本小题满分13分)
如图,已知四棱锥P-ABCD的底面是菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD.
(Ⅰ)求证:PD⊥BC;
(Ⅱ)若AB=6,PC=6,求二面角P-AD-C的大小;
(Ⅲ)在(Ⅱ)的条件下,求异面直线PB与DE所成角的余弦值.