正弦曲线y=sinx通过坐标变换公式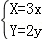 ,变换得到的新曲线为()
,变换得到的新曲线为()
A.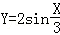 |
B.Y=2sin3X | C. |
D.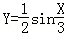 |
对于函数f(x),如果存在锐角θ使得f(x)的图象绕坐标原点逆时针旋转角θ,所得曲线仍是一函数,则称函数f(x)具备角θ的旋转性,下列函数具有角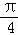 的旋转性的是()
的旋转性的是()
A. |
B.y=lnx | C.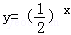 |
D.y=x2 |
将直线y=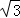 x绕原点逆时针旋转60°,所得到的直线为()
x绕原点逆时针旋转60°,所得到的直线为()
| A.x=0 | B.y=0 | C.y=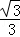 x x |
D.y=﹣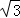 x x |
将直线x+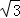 y=0绕原点按顺时针方向旋转30°,所得直线与圆(x﹣2)2+y2=3的位置关系是()
y=0绕原点按顺时针方向旋转30°,所得直线与圆(x﹣2)2+y2=3的位置关系是()
| A.直线与圆相离 | B.直线与圆相交但不过圆心 |
| C.直线与圆相切 | D.直线过圆心 |
将双曲线x2﹣y2=2绕原点逆时针旋转45°后可得到双曲线y= .据此类推可求得双曲线
.据此类推可求得双曲线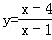 的焦距为()
的焦距为()
A.2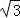 |
B.2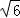 |
C.4 | D.4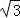 |