我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理如下统计表:
| 男生序号 |
① |
② |
③ |
④ |
⑤ |
⑥ |
⑦ |
⑧ |
⑨ |
⑩ |
| 身高 |
163 |
171 |
173 |
159 |
161 |
174 |
164 |
166 |
169 |
164 |
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择一个统计量作为选定标准,找出这10名具有“普通身高”的是哪几位男生?并说明理由;
(3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中“普通身高”的人数约有多少名?
科学家们测出天鹅座第61颗暗星发射的光线到达地球需3.4×108秒,已知光的速度为3×105千米/秒,求路程。
计算下列各式,结果用幂的形式表示:
(1)(107)3;(2)(a4)8;(3)[(-x)6]3;(4)(x3)4·(x2)5.
某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写所有选购方案(利用树状图或列表方法表示);
(2)已知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示)恰好用10万元人民币,其中甲品牌电脑为A型电脑,求该学校购买了A型电脑几台?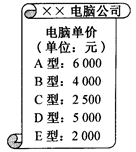
2006年世界杯足球赛德国组委会公布的四分之一决赛门票价格为:一等席300美元,二等席200美元,三等席125美元.某服装公司在促销活动中, 组织获得特等奖、一等奖的36名乘客到德国观看2006年世界杯足球赛四分之一决赛.除去其他费用后,计划买两种门票,用完5025美元,你能设计出最多几种购票方案,供该服装公司选择?并说明理由.
2006年国庆节期间,九年级(2)班的一个综合实践活动小组去A、B两个超市调查去年和今年“十一”期间的销售情况,图中是调查后小敏与其他两位同学进行交流的情景.根据他们的对话,请你分别求出A、B两个超市今年“十一”期间的销售额.