操作与探索：
已知点O为直线AB上一点，作射线OC，将直角三角板ODE放置在直线上方(如图①)，使直角顶点与点O重合，一条直角边OD重叠在射线OA上，将三角板绕点O旋转
（1）当三角板旋转到如图②的位置时，若OD平分∠AOC，试说明OE也平分∠BOC.
（2）若OC⊥AB，垂足为点O(如图③)，请直接写出与∠DOB互补的角
（3）若∠AOC=135°(如图④)，三角板绕点O按顺时针从如图①的位置开始旋转，到OE边与射线OB重合结束. 请通过操作，探索：在旋转过程中，∠DOB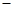
∠COE的差是否发生变化？若不变，请求出这个差值；若变化，请用含有n(n为三角板旋转的度数)的代数式表示这个差.
先化简，再求值：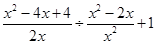 
，其中x满足
．
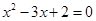已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．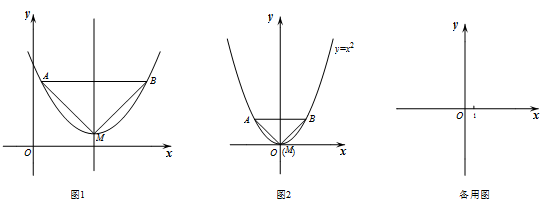
（1）①如图2，求出抛物线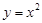
的“完美三角形”斜边AB的长；
②抛物线
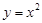与的“完美三角形”的斜边长的数量关系是；
（2）若抛物线
的“完美三角形”的斜边长为4，求a的值；
（3）若抛物线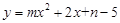
的“完美三角形”斜边长为n，且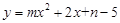的最大值为-1，求m，n的值．
如图，△ABC中，AB=AC，点P是三角形右外一点，且∠APB=∠ABC．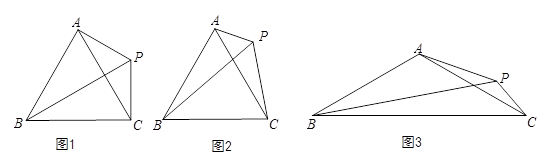
（1）如图1，若∠BAC=60°，点P恰巧在∠ABC的平分线上，PA=2，求PB的长；
（2）如图2，若∠BAC=60°，探究PA，PB，PC的数量关系，并证明；
（3）如图3，若∠BAC=120°，请直接写出PA，PB，PC的数量关系．
在平面直角坐标系xOy中，抛物线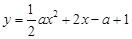
与y轴交于C点，与x轴交于A，B两点（点A在点B左侧），且点A的横坐标为-1．
（1）求a的值；
（2）设抛物线的顶点P关于原点的对称点为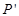
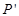，求点的坐标；
（3）将抛物线在A，B两点之间的部分（包括A， B两点），先向下平移3个单位，再向左平移m（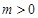
）个单位，平移后的图象记为图象G，若图象G与直线
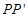无交点，求m的取值范围．
阅读、操作与探究：
小亮发现一种方法，可以借助某些直角三角形画矩形，使矩形邻边比的最简形式（如4：6的最简形式为2：3）为两个连续自然数的比，具体操作如下：
如图1，Rt△ABC中，BC，AC，AB的长分别为3，4，5，先以点B为圆心，线段BA的长为半径画弧，交CB的延长线于点D，再过D，A两点分别作AC，CD的平行线，交于点E．得到矩形ACDE，则矩形ACDE的邻边比为．
请仿照小亮的方法解决下列问题： 
（1）如图2，已知Rt△FGH中，GH：GF：FH= 5：12：13，请你在图2中画一个矩形，使所画矩形邻边比的最简形式为两个连续自然数的比，并写出这个比值；
（2）若已知直角三角形的三边比为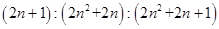
（n为正整数），则所画矩形（邻边比的最简形式为两个连续自然数的比）的邻边比为．