如图所示，光滑半圆形轨道处于竖直平面内，半圆轨道与光滑的水平地面相切于半圆的端点A。一质量为m的小球在水平地面上的C点受水平向左的恒力F由静止开始运动，当运动到A点时撤去恒力F，小球沿竖直半圆轨道运动到轨道最高点B点，最后又落在水平地面上的D点（图中未画出）。已知A、C间的距离为L,重力加速度为g。
（1）若轨道半径为R，求小球到达圆轨道B点时对轨道的压力FN;
（2）为使小球能运动到轨道最高点B，求轨道半径的最大值Rm；
（3）轨道半径R多大时，小球在水平地面上的落点D到A点的距离最大？最大距离xm是多少？
物体A的质量M＝1kg，静止在光滑水平面上的平板车B的质量为m＝0.5kg、长L＝1m。某时刻A以v0＝4m/s向右的初速度滑上木板B的上表面，在A滑上B的同时，给B施加一个水平向右的拉力。忽略物体A的大小，已知A与B之间的动摩擦因数µ＝0.2，取重力加速度g=10m/s2.试求: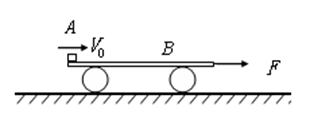
（1）若F=5N，物体A在小车上运动时相对小车滑行的最大距离；
（2）如果要使A不至于从B上滑落，拉力F大小应满足的条件。
如图所示，传送带与水平面之间的夹角为α，并以速度v沿斜面向上匀速运行. 传送带的总长度为L.若将一质量为m的木块轻轻置于传送带上，木块恰处于静止状态. 现将传送带与水平方向之间的夹角增加为2α，且仍以原速度沿斜面向上运行，此时将该木块放在传送带的中央，然后由静止释放，求经多长时间木块滑离传送带.（重力加速度为g）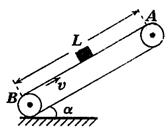
如图所示，重30N的物体，用OC绳悬挂在O点，OC绳能承受的最大拉力为20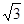
N，再用一绳系在OC绳的A点，BA绳能承受的最大拉力为30N，现用水平力拉BA，可以把OA绳拉到与竖直方向成多大角度？
如图所示，A、B两棒均长l m，A悬于高处，B竖于地面．A的下端和B的上端相距s="10" m．若A、B两棒同时运动，A做自由落体运动，B以初速度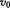
= 20m／s做竖直上抛运动，在运动过程中都保持竖直．问：
(1)两棒何时开始相遇?
(2)擦肩而过(不相碰)的时间?(取g="10" m／s2)．
如图所示，左图表示用水平恒力F拉动水平面上的物体，使其做匀加速运动。当改变拉力的大小时，相对应的匀加速运动的加速度
也会变化，和F的关系如右图所示。
(1)图线的斜率及延长线与横轴的交点表示的物理意义分别是什么?
(2)根据图线所给的信息，求物体的质量及物体与水平面的动摩擦因数；