定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“ —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
等差数列 中,
中,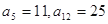 ,则
,则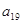 的值为()
的值为()
A.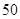 |
B.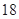 |
C.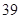 |
D.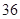 |
若△ABC能被一条直线分成两个与自身相似的三角形,那么这个三角形的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.不能确定 |
在建立两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数
的回归模型中,分别选择了4个不同的模型,它们的相关指数 如下,其中拟合最好的模型是( )
如下,其中拟合最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 |
B.模型2的相关指数 为0.80 为0.80 |
C.模型3的相关指数 为0.50 为0.50 |
D.模型4的相关指数 为0.25 为0.25 |
一等差数列的前n项和为210,其中前4项的和为40,后4项的和为80,则n的值为( )
| A.12 | B.14 |
| C.16 | D.18 |
已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A. =1.23x+4 =1.23x+4 |
B. =1.23x+5 =1.23x+5 |
C. =1.23x+0.08 =1.23x+0.08 |
D. =0.08x+1.23 =0.08x+1.23 |