竖直放置的U形导轨宽为L=1.5m,上端串有电阻R=15Ω。磁感应强度为B=2T的匀强磁场方向垂直纸面向外。金属棒ab质量m=0.1kg,电阻r=3Ω,与导轨接触良好,导轨电阻不计,不计摩擦,从静止释放后保持水平而下滑,g="10" m/s2。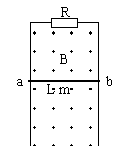
(1)求其下滑的最大速度vm。
(2)求达到最大速度时金属棒两端的电势差Uab。
如图所示,倾角为37℃的足够大斜面以直线MN为界由两部分组成,MN垂直于斜面的水平底边PQ且左边光滑右边粗糙,斜面上固定一个既垂直于斜面又垂直于MN的粗糙挡板。质量为m1=3kg的小物块A置于挡板与斜面间,A与挡板间的动摩擦因数为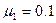 。质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为
。质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为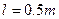 ,此时,细线恰好处于伸直状态。A、B可视为质点且与斜面粗糙部分的动摩擦因数均为
,此时,细线恰好处于伸直状态。A、B可视为质点且与斜面粗糙部分的动摩擦因数均为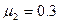 ,它们的水平距离S=7.5m。现A以水平初速度
,它们的水平距离S=7.5m。现A以水平初速度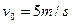 向右滑动并恰能与B发生弹性正撞。g=10m/s2。求:
向右滑动并恰能与B发生弹性正撞。g=10m/s2。求:
(1)A碰撞前向右滑动时受到的摩擦力;
(2)碰后A滑行的位移;
(3)B沿斜面做圆周运动到最高点的速度。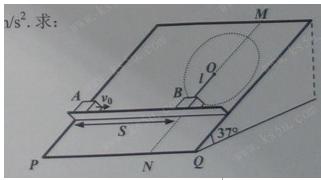
轻质细线吊着一质量为m=0.32kg,边长为L=0.8m、匝数n=10的正方形线图总电阻为r=1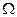 ,边长为
,边长为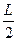 的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
(1)在前t0时间内线图中产生的电动势;
(2)在前t0时间内线图的电功率;
(3)求t0的值。
如图所示,倾角为37℃的足够大斜面以直线MN为界由两部分组成,MN垂直于斜面的水平底边PQ且左边光滑右边粗糙,斜面上固定一个既垂直于斜面又垂直于MN的粗糙挡板。质量为m1=3kg的小物块A置于挡板与斜面间,A与挡板间的动摩擦因数为 。质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为
。质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为 ,此时,细线恰好处于伸直状态。A、B可视为质点且与斜面粗糙部分的动摩擦因数均为
,此时,细线恰好处于伸直状态。A、B可视为质点且与斜面粗糙部分的动摩擦因数均为 ,它们的水平距离S=7.5m。现A以水平初速度
,它们的水平距离S=7.5m。现A以水平初速度 向右滑动并恰能与B发生弹性正撞。g=10m/s2。求:
向右滑动并恰能与B发生弹性正撞。g=10m/s2。求:
(1)A碰撞前向右滑动时受到的摩擦力;
(2)碰后A滑行的位移;
(3)B沿斜面做圆周运动到最高点的速度。
轻质细线吊着一质量为m=0.32kg,边长为L=0.8m、匝数n=10的正方形线图总电阻为r=1 ,边长为
,边长为 的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
(1)在前t0时间内线图中产生的电动势;
(2)在前t0时间内线图的电功率;
(3)求t0的值。
如图所示,倾角为37℃的足够大斜面以直线MN为界由两部分组成,MN垂直于斜面的水平底边PQ且左边光滑右边粗糙,斜面上固定一个既垂直于斜面又垂直于MN的粗糙挡板。质量为m1=3kg的小物块A置于挡板与斜面间,A与挡板间的动摩擦因数为 。质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为
。质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为 ,此时,细线恰好处于伸直状态。A、B可视为质点且与斜面粗糙部分的动摩擦因数均为
,此时,细线恰好处于伸直状态。A、B可视为质点且与斜面粗糙部分的动摩擦因数均为 ,它们的水平距离S=7.5m。现A以水平初速度
,它们的水平距离S=7.5m。现A以水平初速度 向右滑动并恰能与B发生弹性正撞。g=10m/s2。求:
向右滑动并恰能与B发生弹性正撞。g=10m/s2。求:
(1)A碰撞前向右滑动时受到的摩擦力;
(2)碰后A滑行的位移;
(3)B沿斜面做圆周运动到最高点的速度。