阅读下面材料：
小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA="3" ，PB=4，PC=5，求∠APB的度数.
小伟是这样思考的：如图2，利用旋转和全等的知识构造△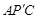
，连接
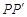，得到两个特殊的三角形，从而将问题解决．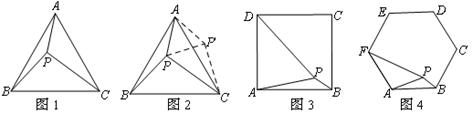
请你回答：图1中∠APB的度数等于 .
参考小伟同学思考问题的方法，解决下列问题：
（1）如图3，在正方形ABCD内有一点P，且PA=
，PB=1，PD=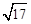
，则∠APB的度数等于 ，正方形的边长为 ；
（2）如图4，在正六边形ABCDEF内有一点P，且PA=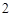
，PB=1，PF=
，则∠APB的度数等于 ，正六边形的边长为 ．
（年湖南张家界10分）如图，在四边形ABCD中，AB＝AD，CB＝CD，AC与BD相交于O点，OC=OA，若E是CD上任意一点，连结BE交AC于点F，连结DF．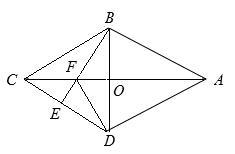
（1）证明：△CBF≌△CDF；
（2）若AC=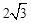
，BD=2，求四边形ABCD的周长；
（3）请你添加一个条件，使得∠EFD＝∠BAD，并予以证明.
（年湖南湘潭10分）△ABC为等边三角形，边长为a，DF⊥AB，EF⊥AC。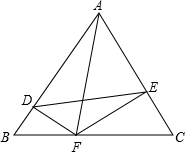
（1）求证：△BDF∽△CEF；
（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系，并探究当m为何值时S取最大值；
（3）已知A、D、F、E四点共圆，已知tan∠EDF=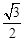
，求此圆直径．
（年黑龙江哈尔滨10分）如图，在四边形ABCD中，对角线AC、BD相交于点E，且AC⊥BD，∠ADB=∠CAD+∠ABD，∠BAD=3∠CBD．
（1）求证：△ABC为等腰三角形；
（2）M是线段BD上一点，BM：AB=3：4，点F在BA的延长线上，连接FM，∠BFM的平分线FN交BD于点N，交AD于点G，点H为BF中点，连接MH，当GN=GD时，探究线段CD、FM、MH之间的数量关系，并证明你的结论．
（年黑龙江大庆9分）如图，等腰△ABC中，AB=AC，∠BAC=36°，BC=1，点D在边AC上且BD平分∠ABC，设CD=x．
（1）求证：△ABC∽△BCD；
（2）求x的值；
（3）求cos36°﹣cos72°的值．
（年贵州六盘水14分）为践行党的群众路线，六盘水市教育局开展了大量的教育教学实践活动，如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形．
活动中测得的数据如下：
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据，求出旗杆的高度．（计算结果保留到0.1，参考数据
，）