如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L⊥直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
试建立适当的直角坐标系,解决下列问题: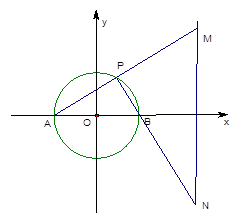
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
如图,直三棱柱 中,
中, 、
、 分别是棱
分别是棱 、
、 的中点,点
的中点,点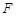 在棱
在棱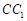 上,已知
上,已知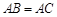 ,
,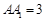 ,
,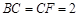 .
.
(1)求证: 平面
平面 ;
;
(2)设点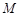 在棱
在棱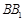 上,当
上,当 为何值时,平面
为何值时,平面 平面
平面 ?
?
(理)已知⊙ :
: 和定点
和定点 ,由⊙
,由⊙ 外一点
外一点 向⊙
向⊙ 引切线
引切线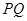 ,切点为
,切点为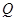 ,且满足
,且满足 .
.
(1)求实数 间满足的等量关系;
间满足的等量关系;
(2)求线段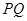 长的最小值;
长的最小值;
(3)若以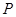 为圆心所作的⊙
为圆心所作的⊙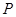 与⊙
与⊙ 有公共点,试求半径取最小值时的⊙
有公共点,试求半径取最小值时的⊙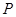 方程.
方程.
(文)已知半径为5的圆的圆心在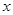 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线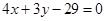 相切.
相切.
(1)求圆的标准方程;
(2)设直线
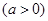 与圆相交于
与圆相交于 两点,求实数
两点,求实数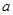 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数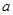 ,使得弦
,使得弦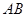 的垂直平分线
的垂直平分线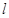 过点
过点 ,
,
如图,在四面体 中,
中, ,
,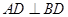 ,点
,点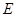 ,
,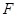 分别是
分别是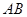 ,
, 的中点.
的中点.
(1)EF∥平面ACD;
(2)求证:平面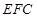 ⊥平面
⊥平面 ;
;
(3)若平面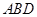 ⊥平面
⊥平面 ,且
,且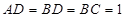 ,求三棱锥
,求三棱锥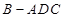 的体积.
的体积.