已知函数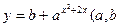 是常数且
是常数且 在区间[—
在区间[— ,0]上有
,0]上有 ,试求a、b的值。
,试求a、b的值。
设全集U=R,集合
(1)求 ;
;
(2)求(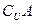 )
) .
.
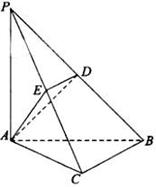
如图,已知点P是三角形ABC外一点,且 底面
底面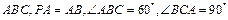 ,点
,点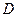 ,
, 分别在棱
分别在棱 上,且
上,且 。。
。。
(1)求证: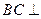 平面
平面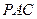 ;
;
(2)当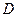 为
为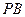 的中点时,求
的中点时,求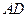 与平面
与平面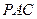 所成的角的大小;
所成的角的大小;
(3)是否存在点 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
AN⊥PC于N.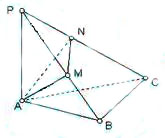
(1)求证:BC⊥面PAC;
(2)求证:PB⊥面AMN.
(3)若PA=AB=4,设∠BPC=θ,试用tanθ表示△AMN的面积,当tanθ取何值时,△AMN的面积最大?最大面积是多少?
如图,点P是边长为1的菱形ABCD外一点,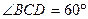 ,E是CD的中点,
,E是CD的中点,
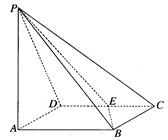
(1)证明:平面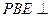 平面PAB;
平面PAB;
(2)求二面角A—BE—P的大小。